Vorticity Confinement で渦度を強調する

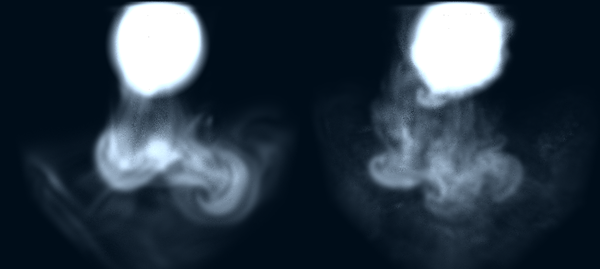
数日前から作っていた冷気のシミュレーションが完成しました。冷たいボールのような何かから舞い降りる冷気を観察できます。流体計算は Stable Fluids をベースに、移流計算に MacCormack 法を用いて Vorticity Confinement を加えたものになっています。

シミュレーションは WebGL を用いて全て GPU 上で行われます。あまり古くないPCやスマホならそれなりに快適に動作してくれるはずです。

Play: Chill

この記事ではシミュレーション中で使われている手法の Vorticity Confinement について解説します。

速度場の数値拡散

前回の記事で説明した通り、物理量は移流によって数値拡散を起こし、値が鈍って均一になっていきます。MacCormack 法は数値拡散を起こしにくい移流計算手法ですが、速度場の移流に適用するとアーティファクトの影響でシミュレーションが不安定化してしまったため、速度場は普通の Semi-Lagrangian 法で移流させることにしました^[1]。

密度場が拡散を起こすと流体がぼやけて消えていくという視覚的な効果が得られますが、速度場は直接見えるものではなく、拡散を起こすと流体の運動に変化が起こります。

実は速度場の拡散は流体の粘性に直結しており、速度場の拡散が激しいほど流体は強い粘性を示します。流体の運動方程式である Navier-Stokes 方程式（の簡易版）は

\frac{\partial \bm u}{\partial t}+(\bm u\cdot\nabla)\bm u=-\frac1\rho\nabla p+\nu\nabla^2\bm u+\bm f

という形をしており、\nu\nabla^2\bm u の部分は流体の粘性を司るため粘性項と呼ばれます。この項は「速度場 \bm u を強さ \nu でぼかせ！」と言っており、この式からも速度場の拡散とは粘性に他ならないことが分かります。

粘性が高いと流体に何が起こるでしょうか。実は色々興味深いことが起こるのですが、それらは置いておいて簡単な面に着目すると……細かい渦が消えます。水などの粘性の小さな流体は、普段は流れているときにありとあらゆる方向に無茶苦茶に渦を巻く乱流という状態にあります。しかし、速度場の数値拡散により生じる粘性（＝数値粘性）によって細かい渦は即座に消えてしまうため、Stable Fluids ではこうした現象を再現することができません。

乱流をできるだけうまく計算に取り入れたい場合は乱流モデルというものを導入することが多いですが、用途が CG 作成だったりして「そこまで正確じゃなくていいけど全体的にもうちょっとくるくるしてほしいな……」というときに使えるのが Vorticity Confinement です。

Vorticity Confinement

※ Vorticity Confinement は Steinhoff によるオリジナルの手法 (VC1) と後に改良された手法 (VC2) の2種類があるようですが、本稿では VC1 のみを扱います。

Vorticity Confinement の基本的な考えは「速度場が拡散して渦が消えるなら、速度場の渦を強化するように外力を加え続ければいいんじゃね？」というところにあります。

しかし、外力の計算方法がトリッキーで、式を見たりソースコードを読んだりするだけだと一見して何がどうなってるのかよく分かりません。

結論から言うと、\bm u を速度場、\varepsilon を Vorticity Confinement の強さを決める定数として、外力は次の式で求められます。

\varepsilon\frac{\nabla\lvert\nabla\times\bm u\rvert}{\lvert\nabla\lvert\nabla\times\bm u\rvert\rvert}\times(\nabla\times\bm u)

？

よく分からなかったと思います。自分も最初見たときはなぜこれでうまくいくのか分かりませんでした。これからこの式の意味を追っていきます。

まず \nabla\times\bm u ですが、これは速度場の回転を表します。ベクトル解析でお馴染みの演算子の一つですね。

\bm\omega=\nabla\times\bm u = \left(
\dfrac{\partial u_z}{\partial y} - \dfrac{\partial u_y}{\partial z},\ 
\dfrac{\partial u_x}{\partial z} - \dfrac{\partial u_z}{\partial x},\ 
\dfrac{\partial u_y}{\partial x} - \dfrac{\partial u_x}{\partial y}
\right)

このベクトルは渦度と呼ばれ、\bm\omega で表されます。渦度からは、その場所で速度場がどの方向にどれだけ渦を巻いているかの情報を得ることができます。渦の強さは渦度の絶対値 \lvert\bm\omega\rvert で、渦の方向は \bm\omega/\lvert\bm\omega\rvert で得ることができます。

渦の方向は渦の回転軸を表します。すなわち、\bm\omega が y 軸方向を向いているとき、速度場は xz 平面上に渦を巻いています。渦を巻く向きは右ねじ方向です。日本で観測される台風は反時計回りに回っているので、台風の渦度は地球から飛び出す法線方向を向いていることになります。

渦度を用いて Vorticity Confinement の外力を書き直すと次のようになります。

\varepsilon\frac{\nabla\lvert\bm\omega\rvert}{\lvert\nabla\lvert\bm\omega\rvert\rvert}\times\bm\omega

少し見通しが良くなりました。次に \nabla\lvert\bm\omega\rvert に着目します。

\lvert\bm\omega\rvert は渦の強さを表す量だったので、その勾配 \nabla\lvert\bm\omega\rvert は渦がより強くなる方向を向きます。基本的に速度場の渦は渦の中心に向かうほど強くなるので、\nabla\lvert\bm\omega\rvert は渦の中心へ向かう方向のベクトルを表すことになります。

すると、そのベクトルを自身の長さで割ったベクトル \nabla\lvert\bm\omega\rvert/\lvert\nabla\lvert\bm\omega\rvert\rvert は、渦の中心方向を向く単位ベクトルということになります。これを \bm n で表すことにしましょう。

\varepsilon\bm n\times\bm\omega

だいぶシンプルになりました。最後に \bm n\times\bm\omega について考えます。\bm n は渦の中心へ向かう単位ベクトル、\bm\omega は渦の回転軸と強さを表すベクトルです。これらの外積は下図のようになります。

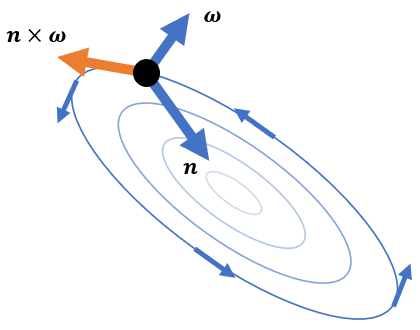
元々あった渦を強調する方向のベクトルが得られました。\bm n は単位ベクトルなので、\bm\omega が大きいほど、そして \bm n と \bm\omega が直交しているほど外積は大きなベクトルになります。つまり、

• 元の渦度が大きいほど
• 渦の中心から回転軸に垂直に広がる平面に近いほど

大きなベクトルが得られることになります。このベクトルを Vorticity Confinement の強さ \varepsilon で調整したものが外力となります。

確かにうまくいきそう

こうして数式の全体を理解してみると、Vorticity Confinement は確かにうまく働きそうという直観を得ることができます。こうした直観はアルゴリズムの理解に役立つだけでなく、実装をバグらせたときに「どこで何を間違えたのか」といった分析をする際にも大いに役立ちます。

Vorticity Confinement の効果のほどはぜひ Chill の Vorticity パラメータ（ \varepsilon に相当）を変化させて確かめてみてください。パラメータを大きくするとモクモク感が強調されるのが分かると思います。