虹色のゼリーを粉砕できるシミュレーションを作りました。
シミュレーションは WebGL 2.0 の機能をふんだんに利用した GPGPU で行われています。機種依存のバグが多すぎてスマホの対応が大変でした(まだ対応できていないスマホもあります)。
概要
超弾性体を GPGPU で計算、メッシュ化して適当に着色して描画しています。シェーダは全部 HGSL で書かれています。HGSL は半分これのために作ったようなものでもあり、おかげでシェーダの開発は快適でした。WebGL の仕様自体にはだいぶ苦しめられましたが……。
シミュレーション手法には MLS-MPM を用いました。超弾性体のモデルは Neo-Hookean モデルを使用しています。
この記事では MLS-MPM について詳しく書いていこうと思います。ついでに実装において使用したテクニック等についても解説します。
Material Point Method
まず MLS-MPM とはなんぞやということになりますが、これには前身の MPM (Material Point Method, 物質点法) という手法があります[1]。これを理解しないことには始まらないので、まずは MPM の説明をします。
さて、MPM については SIGGRAPH 2016 の Course として公開された非常によくまとまっているノートがネット上に公開されています。そこそこの英語と工学部レベルの数学を理解できるのであれば、時間をかけてでもこのコースノートをきちんと読み切ることを強く推奨します[2]。筆者も MPM の大部分をこのコースノートで学びました。
The Material Point Method for Simulating Continuum Materials
本当は説明のすべてをコースノート(と論文)に譲りたいくらいなんですが、この記事では恐らくこれからコースノートを読む人にとっても役に立つであろう、ふわっとした全体像と関連手法との関係性の理解を提供することにします。理解を深めるためにはより詳細な文献にあたり、細かい理論のステップをぜひ確認していただければと思います。
また、MLS-MPM の実装にあたっては、こちらのページが非常に参考になりました。論文だけから実装まで落とし込むのは非常に大変なので、ステップごとに実装付きで解説してくれるのは本当に助かりました。
Thanks a lot!
どんな手法か
平たく言うと格子法と粒子法のハイブリッドになります。
格子法
格子法とは全ての物理量を格子(グリッド)点上に格納し、必要に応じて補間などを行いながら計算を進めていく手法になります。特に粒子は出る幕がありません。格子だけで全部済んでしまうので。
格子法で有名な手法としては、VOF 法や Stable Fluids などがあります。
Works で公開している Chill も格子法です。
格子法の利点として、
- 隣接関係の構造が単純明快(格子なので)
- GPGPU による並列計算が容易
- 空間を埋め尽くすような表現(気体など)が得意
- 精度の理論保証がしやすい
などが挙げられます。逆に、
- 質量の保存が非自明
- 数値拡散の影響が大きい
- 局所的な計算が苦手
などの難点が挙げられます。
粒子法
粒子法とは、全ての物理量を動き回る粒子上に格納し、粒子同士の相互作用を通してシミュレーションを進めていく手法です。格子の出る幕は……一応あります。近傍粒子探索(≒衝突判定)なんか格子がないと悲惨なことになるので。
粒子法で有名な手法としては、SPH 法や MPS 法などがあります。
Works で公開している Fluid も粒子法です。
粒子法の利点として、
- 質量の保存が自明
- 移流による数値拡散がゼロ
- 局所的な計算が得意
などが挙げられます。逆に、
- 隣接関係が動的で複雑
- GPGPU による並列計算が困難(特に近傍粒子探索)[3]
- 空間を埋め尽くすような表現(気体など)が非効率がち
- 精度の理論保証がしづらい
などの難点が挙げられます。
ハイブリッド
両者のメリットを組み合わせて最強!……みたいなことにはならないのですが、それなりにいい感じには落ち着いています。
MPM では、移流計算を粒子で、それ以外を格子で行います。各粒子は質量を保持しているので、全体の質量保存則は移流を経ても自明に満たされます。一方、力の計算などはすべて格子を通して行うので、空間の規則正しさが効いていい感じになってくれます。GPGPU 化も(素の粒子法に比べれば)だいぶ易しくなっています。
ハイブリッド化に伴い、粒子と格子を行き来する方法も必要になってきます。MPM では、Particle to Grid と Grid to Particle というステップを通して格子-粒子間の情報の受け渡しを行います。
具体的には、各タイムステップの最初に Particle to Grid で粒子の運動量の情報を格子に渡し、続いて格子上で各粒子からの力の適用・速度の計算を行い、Grid to Particle で速度の情報を粒子に戻し、粒子の座標を更新する、という流れです。
最終的には粒子から始まり粒子に終わっているので、途中に出現した格子はあくまで粒子間相互作用計算のための計算用紙に過ぎない、と捉えることもできます。まあこの辺は自由です。
粒子法との大きな違いとして、直接的に粒子間の相互作用を計算しないので近傍粒子探索が不要という点があります。陽的に計算される粒子法のシミュレーションにおいては、近傍粒子探索は計算時間のうちかなりの部分を占めることになるため、計算時間の短縮が見込めます。
実際に MPM のパフォーマンスの高さを確認できるデモを作りました[4]。GPU ではなくシングルスレッドの CPU で動いています。SPH 法でこのパフォーマンスを出すのはまず無理だと思います。
近傍粒子探索が不要で高速な計算が可能である MPM ですが、後に見ていくようにその性質ゆえに普通の粒子法よりも扱いづらくなっている点も多々存在します。
計算の流れ
各時間ステップでの計算の流れは次のようになります。今回は陰的な時間積分やグリッドと他の物質の衝突などについては考えません。
- Particle to Grid
- Velocity Computation
- Velocity Update
- Deformation Gradient Update
- Grid to Particle
- Particle Advection
Particle to Grid
粒子の持っている情報をグリッド(=格子)に分配します。基本的には各粒子の運動量と質量がその粒子に近接するグリッドのセルへと分配されます。
この際のイメージですが、まず空間全体が無数の格子によって立方体(2次元の場合は正方形)に区切られている様子を想像してください。区切られた一つ一つの立方体(または正方形)のことをセルと呼びます。そして、セルの情報は全てセルの中央に集約されているものと考えてください(このような格子をコロケート格子 (collocated grid) といいます)。セルの位置を考える必要が出てきたときも、セルの中央の座標がセルの位置であるとして考えます。
次に、空間を飛んでいる一つの粒子を考えます。空間はすべて格子に分割されているので、この粒子はある一つのセルに属していることになります[5]。この粒子の情報は、この粒子が属しているセルと、その周囲のセルの合計 27 セル(2次元の場合は 9 セル)に分配されることになります。
粒子から格子に情報を分配する際は、粒子とセルの相対位置によって定まる重み係数に従って分配を行います。重み係数は粒子とセルの位置が近いほど大きくなり、かつ全てのセルに対する重み係数の総和は 1 となります。したがって、重み係数に従った分配後の値も総和は一定に保たれます。
よく使われる重み係数の計算方法は次の通りです。まず、1次元の場合の重み係数 N\colon \mathbb R\to\mathbb R を定義します。
N(x) = \begin{cases}3/4-x^2 & (0\leq\lvert x\rvert\lt1/2)\\
(3/2-\lvert x\rvert)^2/2 & (1/2\leq\lvert x\rvert\lt3/2)\\
0 & (3/2\leq\lvert x\rvert)
\end{cases}次に、2次元・3次元の場合の重み関数 N_2\colon \mathbb R^2\to\mathbb R, N_3\colon \mathbb R^3\to\mathbb R を次のように定義します。
N_2(\bm r) &= N(r_x)N(r_y) \\
N_3(\bm r) &= N(r_x)N(r_y)N(r_z)計算すると分かりますが、近接するセルの重みの総和は次元によらず 1 になります。ただし、N の引数は 1 が 1 セル分の大きさを表すようにスケーリングしてください。セル-粒子間の重み係数を、この重み関数に従い決定します。決定された重み係数に従い、粒子の運動量と質量を近傍のセルに分配します。
Velocity Computation
格子には運動量と質量が分配されているので、各セルについて運動量を質量で割って速度を計算します。ただし、質量がゼロである(あるいはゼロに十分近い)セルについては速度をゼロとします。
Velocity Update
各セルに働く力を計算し、セルの速度を更新します。このフェーズが物体の挙動を決定します。
計算方法はいくつかあるのですが、各粒子が持つ応力テンソルを用いた方法が弾性体・流体ともに利用でき、汎用性が高いです。
粒子 p が持っているコーシー応力テンソルを \bm\sigma_p とし、粒子 p の近くにあるセルをセル i とします。このとき、セル i には次の力 \bm f_{ip} がかかります。
\bm f_{ip} = -V_p\bm\sigma_p\nabla w_{ip}ただし、V_p は現在の粒子 p の占める体積、w_{ip} はセル i と粒子 p 間の重み係数です(偏微分は粒子の座標について行います)。
今は各セルにかかる力の総和を知りたいので、セル i を固定して、セル i の近傍に存在する粒子について和を取ります。すると、セル i にかかる力の総和 \bm f_i は、
\bm f_i = -\sum_pV_p\bm\sigma_p\nabla w_{ip}と表されます。こうして求めた \bm f_i を使って、セル i の速度を
\bm v_i \gets \bm v_i + \Delta t\frac{\bm f_i}{m_i}と更新することができます。重力などの外力がある場合には、それらも \bm f_i に含める必要があります。また、境界条件の処理もこの段階で行います。
Deformation Gradient Update
MPM では、各粒子はその位置における局所的な変形の情報を持っています。この情報は変形勾配テンソルと呼ばれ、シミュレーションの次元と同じ次元の正方行列として表されます。
簡単に変形勾配テンソルについて説明します。
まず変形とは何でしょうか。変形について議論するためには、変形する前の基準となる形状を決めておかなければなりません。
手元にしぼんだ風船があるとしましょう。この状態を変形前の状態とします。
次に風船を膨らませて、どこかに置いたとします。しぼんだ状態の風船上に存在する点 \bm X を考えます。すると、膨らんだ状態の風船上にも対応する点 \bm x を考えることができます。\bm x は \bm X に対応して決まるので、それぞれの \bm X に \bm x を対応させる写像 \phi が存在します。すなわち \bm x=\phi(\bm X) が成り立ちます。あらゆる変形は写像 \phi によって必要十分に決定されるため、\phi とは変形そのものであると考えることができます。
続いて変形勾配を考えます。一般に \phi は(滑らかな)非線形写像であり、全体の変形に対する全ての情報を与えますが、そのまま計算で扱うには不向きであり、局所的な変形の情報を与える変形勾配の方が多く用いられます。
再びしぼんだ風船上の点 \bm X を決め、\bm X を始点とする真っすぐで短い矢印を好きなように風船に描きます。これをベクトル \bm V で表します。\bm V は向きと大きさの情報を持ちますが、始点の位置情報は持たないことに注意してください。
その後風船を膨らませると、同じように膨らんだ風船上にも \bm x を始点とする矢印が現れます。元の矢印が十分短ければ、膨らんだ風船上の矢印も真っすぐであるとみなすことができ、ベクトル \bm v で表すことができます(同じように、\bm v は始点の位置情報を持たないことに注意してください)。
これらのベクトル \bm V と \bm v を、\bm v=\bm F(\bm X)\bm V の形で関係付けるのが変形勾配テンソル \bm F(\bm X) です。変形勾配テンソルはしぼんだ風船上の点 \bm X のみに依存し、\phi を用いて次のように表されます。
\bm F(\bm X) = \frac{\partial\phi}{\partial\bm X}(\bm X)変形勾配テンソルは2階のテンソルであり、行列として表すことができるので計算にも向いています。
物質が変形していない状態では変形勾配テンソル(を表現する行列)は単位行列であり、計算が進み物質が変形するにしたがって行列の値も変化していきます。

画像は各粒子の位置にある正方形を、粒子が持つ変形勾配テンソルで変形させて描画したものです。変形勾配テンソルが局所的な変形を表す理由がよく分かるのではないかと思います。
粒子 p が持つ変形勾配テンソル \bm F_p は次のように更新されます。
\bm F_p \gets\left(\bm I+\Delta t\sum_i\bm v_i(\nabla w_{ip})^T\right)\bm F_p添え字 i はセルに対する総和を表します。
Grid to Particle
セルの速度を粒子に移し、粒子を動かします。
粒子の運動量を近傍のセルに分配したのと同じ重みを使い、各セルの速度の重み平均を取って粒子の速度とします。
\bm v_p \gets \sum_i w_{ip}\bm v_i\bm v_p は粒子 p の速度、\bm v_i はセル i の速度です。
最後に、粒子の座標を更新して完了です。
\bm x_p \gets \bm x_p + \Delta t\bm v_pPIC から APIC へ
次に MLS-MPM を構成する一大要素である APIC (Affine Particle-in-Cell) 法について説明します。
PIC
前述の MPM には一つ大きな問題があります。それは、粒子の速度がものすごい速さで拡散するという点です。この拡散は角運動量を失わせるため、振動が減衰するだけでなく、物体の回転もあっという間に止まってしまい現実味がありません[6]。
この原因は粒子の速度をグリッドに移し、再びグリッドから速度を拾ってきて粒子の速度としている点にあります。
- 粒子の速度を近傍のセルに重みを付けて分配する
- 重みを付けた分配なので、ぼかしと同じ効果があり、拡散を起こします
- 近傍のセルの速度の重み付き平均を粒子の速度とする
- 拡散を起こした速度の重み付き平均を取るので、やはり拡散したままです
この方式は Particle-in-Cell (PIC) 法で使われているため、しばしば PIC や PIC 法[7]などと呼ばれます。
FLIP
後に、PIC の欠点である過度な散逸を補うため、FLIP と呼ばれる方式が考案されました。これも PIC と同じく Fluid Implicit Particle (FLIP) 法で用いられている移流方式のため、しばしば単に移流方式だけを指して FLIP と呼ばれることがあります。
FLIP では、Grid to Particle で粒子の速度を更新する際に、粒子の速度を丸々上書きはせず、格子上で生じた速度の差分だけを拾ってきて粒子に適用します。
話を簡単にするために、粒子とセルがそれぞれ一つだけ存在している例を考えます。粒子の速度を \bm v_p、セルの速度を \bm v_i と、粒子とセルは重み係数 1 で繋がっているとします。
最初に粒子の速度を格子に移します。粒子とセルが各一つだけ、重み係数も 1 なので単純な代入と同じ結果になります。
\bm v_i \gets \bm v_p次に、格子に働く力によってセルの速度が \bm v_i から \bm v'_i に変化したとします。PIC ではその後、Grid to Particle の計算フェイズで粒子の速度を格子の速度で置き換えます。
\bm v_p \gets \bm v'_iしかし、FLIP では単純な置き換えはせず、格子上の速度の差分を粒子の速度に適用(加算)します。
\bm v_p \gets \bm v_p + (\bm v'_i - \bm v_i)今回は \bm v_i=\bm v_p なので結果的に PIC と FLIP の結果は一致しますが、一般には両者は異なるものになります。例えば格子上で一切速度変化が起きなかった場合、PIC では速度の拡散が生じますが、FLIP では粒子の速度が変更されないため拡散が起きません。これにより、速度の数値拡散の問題は解決……したといえばしたのですが、別の問題が生じることになります。
FLIP の不安定性と混ぜ合わせ
FLIP を使うと計算が不安定になります。計算が爆発してしまうような不安定性ではないのですが、本来粒子が静止すべきような状況下であっても動き続け、まったく安定して止まってくれず、細かい振動がシミュレーション結果に乗ったような挙動になってしまいます。
PIC では粒子の速度は格子に転送されたあと、いわば一度「完全に記憶を失い」、格子上の速度場のみを用いて再計算されます。
一方 FLIP では、粒子の速度は格子に転送されたあとも記憶され続け、格子の情報を記憶された粒子の情報に「足し込む」形で粒子の速度が更新されます。
この前のステップの粒子の速度が残り続けるという FLIP の性質が計算を不安定化させる一つの要因になっています。
FLIP の不安定性を緩和するため、PIC による速度の計算結果を FLIP による速度の計算結果に数パーセントほど混ぜ合わせるという手法が編み出され、APIC が発明されるまでの間、長らく使われてきました。しかし、少しでも PIC を混ぜてしまうとやはり散逸が生じてしまうため、直接 PIC を使うよりはだいぶマシになるものの、角運動量は徐々に減少していきます。
APIC
2015 年に Affine Particle-in-Cell (APIC) 法が発明されました。この手法は驚異的な威力を発揮し、PIC と FLIP がそれぞれトレードオフのように抱えていた欠点を一度に、しかも完璧に克服してしまいました。
- APIC では運動量、角運動量を完全に保存するだけでなく、剪断方向の速度変化も非常に精度よく保存します。
- FLIP のように前ステップの速度を記憶せず、格子上の速度場のみから粒子の速度を計算するため、計算は完全に安定します。
現在ではよほどの理由がない限り PIC/FLIP による移流計算を行うメリットはないように思います。APIC が完全な上位互換になってしまったためです。
APIC が PIC/FLIP と決定的に異なる点は、粒子が通常の速度に加えて行列の形で表される“速度”を保持している点です。この追加の情報を活用することにより、速度の散逸を大きく抑えることができます。
Particle to Grid (APIC)
APIC では、粒子の運動量を近傍のセルに分配する際の運動量の評価方法が異なります。通常の場合は、粒子 p がセル i に分配する運動量は
w_{ip}m_p\bm v_pと、粒子の運動量 m_p\bm v_p に重み係数 w_{ip} を掛けただけになりますが、APIC では次のようになります。
w_{ip}m_p(\bm v_p+\bm B_p(\bm D_p)^{-1}(\bm x_i-\bm x_p))ここで、\bm x_i, \bm x_p はそれぞれセル i と粒子 p の位置ベクトル、\bm B_p は粒子 p が追加で持っている行列状の速度であり、\bm D_p は次で定まる行列です。
\bm D_p = \sum_iw_{ip}(\bm x_i-\bm x_p)(\bm x_i-\bm x_p)^Tただし、前述の重み係数を使っている場合は \bm D_p の形は簡単になり、\bm D_p = (1/4)\Delta x^2\bm I が成り立ちます。\Delta x は格子の間隔です。これは単位行列のスカラー倍なので、逆行列を乗じる代わりに単純に全要素を 4/\Delta x^2 倍すればいいことになります。
肝心の \bm B_p はというと、これは Grid to Particle フェイズで計算されます。Grid to Particle フェイズで計算された \bm B_p を粒子に保存し、移流させてから次の時間ステップに持ち越して利用する、という形になるわけですね。
Grid to Particle (APIC)
粒子 p の速度 \bm v_p はこれまで通り計算します。行列 \bm B_p は次の式に従い計算します。
\bm B_p = \sum_i w_{ip}\bm v_i(\bm x_i-\bm x_p)^Tこれらの変更を前述の MPM のアルゴリズムに取り入れることで、移流計算の方式を PIC から APIC に変更し、速度の散逸を大幅に抑えた滑らかで安定した計算が可能になります。
Affine とは
余談ですが、affine(発音はアファイン、日本語ではアフィンと書かれる)とは数学で「線形変換+平行移動」を意味する形容詞であり、affine transformation(線形変換に平行移動を加えた変換), affine subspace(線形部分空間を平行移動したもの)などのように用いられます。
APIC の論文では \bm v_p と \bm B_p を合わせて affine velocity と呼んでおり、これは \bm v_p を平行移動にあたる成分、\bm B_p を線形変換にあたる成分、とすることで理解することができます。「通常の速度は粒子を平行移動させる速度であるが、行列として表される速度は粒子を線形変換する速度である」ということになります。
実際、論文中には affine velocity は剛体運動における速度である「並進速度+角速度」の一般化である、と受け取れる説明があります。
MLS-MPM
大変長かったですが、ここまできてようやく MLS-MPM を説明する準備が整いました。
Affine Velocity の正体
MLS-MPM の発表論文において、APIC で用いられていた affine velocity の数学的な正体が明かされることになります。
実は、APIC における粒子 p の速度の行列成分(ただし、\bm B_p そのものではなく \bm B_p(\bm D_p)^{-1})は、粒子位置における速度ベクトルの勾配を移動最小二乗法 (Moving Least Squares, MLS) で求めたものに一致するというのです。
Moving Least Squares
MLS とは、Least Squares(最小二乗法)の結果を局所的に得るため、適当な重み関数を用いて各データ点に重みを付けて最小二乗法による(主に多項式の)フィッティングを行う手法です。
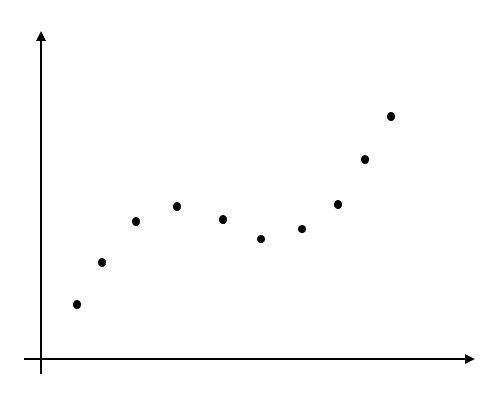
例えばこんな感じでデータ点が並んでいるとします。
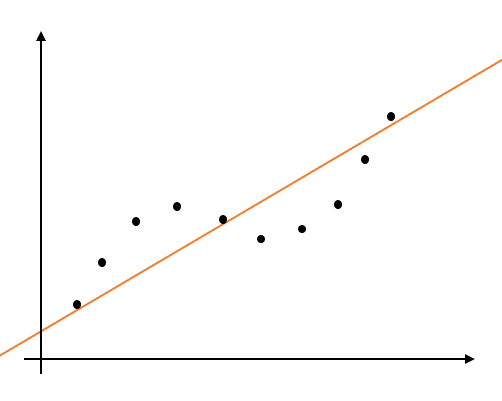
普通に最小二乗法で直線のフィッティングを行うとこんな感じになります。
しかし、全体のフィッティング結果には興味がなく、真ん中あたりのデータに対してだけフィッティングを行いたいとします。

そこで、各データ点に重み係数を設定し、近くのデータの重みが 1 に、遠くのデータの重みが 0 に近づくようにします。
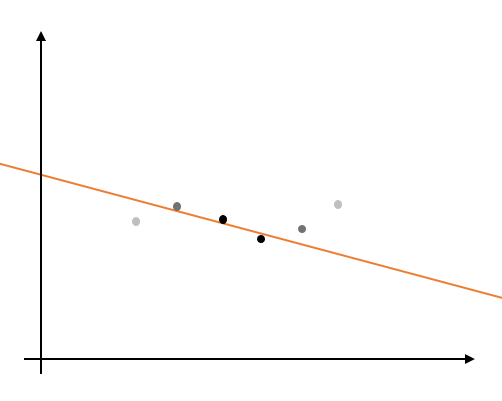
この重みを設定したうえで、最小二乗法によるフィッティングを行うとこのような結果が得られます。
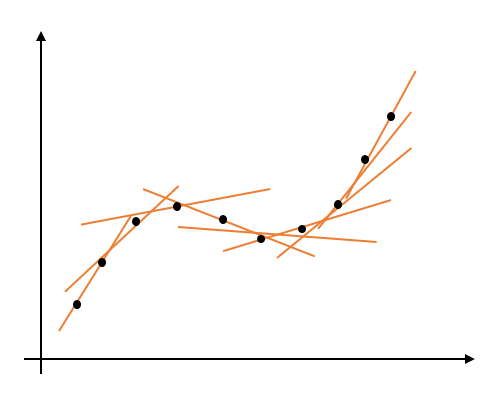
これを各点で行うことで、最小二乗法による局所的なフィッティング結果を得ることができます。これが移動最小二乗法です。
これと同じ原理で、
- フィッティングの評価点を粒子
- データ点を近傍のセル
- 各セルの重みを重み関数による値
で速度場の勾配を計算すると、速度場の勾配として \bm B_p(\bm D_p)^{-1} と同じ値が得られます。
RE: Particle to Grid (APIC)
APIC では次の運動量をセルに分配していました。
w_{ip}m_p(\bm v_p+\bm B_p(\bm D_p)^{-1}(\bm x_i-\bm x_p))\bm B_p(\bm D_p)^{-1} が速度場の勾配だとすれば、
\bm v_p+\bm B_p(\bm D_p)^{-1}(\bm x_i-\bm x_p)は粒子 p が持つ速度場の一次近似のセル i における評価ということになります。これで APIC の物理的・数学的な意味がはっきりしました。
MPM から MLS-MPM へ
さて、MPM では離散化の際に勾配を得るため、重み関数の直接の微分を行っています[8]。ここでは離散化の式の導出は追いませんが、重み関数の微分を行った結果はセルにかかる力の式に現れています。
\bm f_i = -\sum_pV_p\bm\sigma_p\nabla w_{ip}この式に出てくる \nabla w_{ip} がそれです。
一方 APIC で計算される速度場の勾配は、重み関数の微分ではなく MLS による重み関数を使ったフィッティングの結果として得られていました。つまり、かたや重み関数の微分を行い、かたや重み関数によるフィッティングを行っていたわけです。
そこで、MLS の考えを推し進め、MPM の離散化においても重み関数の微分を行わずに MLS によるフィッティングで偏微分を計算してしまおうといって生まれたのが MLS-MPM です。
この試みは非常にうまくいき、結果として MLS-MPM は MPM よりもシンプルで、計算が高速になり、APIC と整合した手法となりました。
MPM と MLS-MPM の違いは以下のようにまとめられています(作者の GitHub のリポジトリより引用)。

source: https://github.com/yuanming-hu/taichi_mpm
\bm B_p(\bm D_p)^{-1} ( = \bm C_p) が速度場の勾配であることが判明したため、変形勾配テンソルを更新する際に計算されていた速度場の勾配もこの行列で置き換えられています。また、セルに働く力を計算する式も重み関数の微分を用いない形になっています。
WebGL 2.0 による実装
ついに MLS-MPM を WebGL で実装する際の話ができます。
グリッド上の計算については特に難しいところはなく、通常の格子法と同じようにテクスチャにデータを格納し、fragment shader で必要な処理を書いてやればよいです。問題は Particle to Grid のように粒子のデータを格子に書き込む処理です。
fragment shader による計算では、処理が開始した時点でデータの書き込み先がすでに決定されています。そのため、好きな位置にデータを書き込む処理 (= scatter) が原理上できません。
WebGL でデータの scatter を行うことができる唯一の手段として、vertex shader を使った点の描画があります。
Vertex Shader による Scatter 計算
vertex shader では、描画対象の図形の頂点の座標を決定します。続いて fragment shader で、決定された画面上の座標における色を決定します。
勘のいい方はすでに気付かれたと思いますが、vertex shader を使って書き込み先の座標を gl_Position に指定することで、好きな位置に fragment shader でデータを書き込むことができます。
しかし、Particle to Grid のフェイズでは、単なる書き込みではなく、各粒子から分配された運動量の総和を求める必要があります。これを可能にするのが OpenGL のブレンディング機能です。
Z buffer による深度テストを無効にし、gl.blendFunc(gl.ONE, gl.ONE) を呼び出すことでブレンディング方法を加算合成にします。すると、全ての同じ場所への書き込みは自動的に和がとられることになります。こうして Particle to Grid の計算が GPU 上でできるようになります。
Transform Feedback
MLS-MPM では粒子間のデータ参照が全く必要ないため、粒子のデータをテクスチャに保存せず、Vertex Buffer Object 上に保存しておくことができます。
すると、WebGL 2.0 から使えるようになった transform feedback を用いて粒子の計算を行うことができるようになります。VBO の方式をインターリーブにしておけば、少なくとも最大で 64 要素までの書き込みを一度に行うことができ[9]、テクスチャを用いるよりも効率的な計算が可能になります。
同じく WebGL 2.0 でサポートされた multiple render targets (MRT) を用いると少なくとも最大 4 テクスチャまで同時に書き込みを行うことができますが、各テクスチャは 4 チャンネルまでしか持てないため、16 要素までの書き込みしかできません。
Geometry Instancing
こちらも WebGL 2.0 から標準で使えるようになった機能で、vertex attribute を再利用しながら多数の図形を描画することが可能になります。transform feedback と組み合わせることで、より効率的に計算を行うことが可能になります。
geometry shader がない分を transform feedback と geometry instancing でどうにかカバーできたという印象です。どちらか一方でも欠けていたら重大なパフォーマンスの問題を引き起こしていたと思います。
メッシュの描画
作成したシミュレーション上では物質が千切れると同時にメッシュも千切れていますが、これが非常に大変でした。細かく説明するとこれだけで記事が一つできてしまうため詳細は省略しますが、かなり複雑なことをやっています。
処理が複雑すぎて GPU ではできないと判断したため、トポロジーの変化を CPU で、トポロジーの情報に基づく頂点座標の計算を GPU で行っています。
一度千切れた粒子は戻ることがないため三角形の数は単調増加であり、VBO を拡張しながら影響を受けた粒子に対応する頂点だけデータを更新することで CPU 側の処理時間を最小限にとどめています。
残念ながらメッシュの描画では他の粒子のデータにアクセスする必要が出てきてしまうので、一度必要なデータをテクスチャに書き出してから vertex texture fetch でデータを取得しています。
MLS-MPM に思うこと
ここからは、実際に MLS-MPM を使ってみて思ったこと、通常の粒子法との違いなどを書き留めていきます。
ちぎれる
今回は千切れるゼリーをシミュレーションしましたが、実はこれ、わざと千切っているわけではないんです。勝手に千切れてしまうんです。
計算に使用した Neo-Hookean モデルは超弾性体と呼ばれる物質のモデルで、本来千切れることはありません。伸びれば伸びた分だけ応力が強くかかるようになるだけです。粒子法においては、何もしなければ弾性体を計算しても千切れることがないのは当然であり、破断を計算に入れたければそれ用の処理を書く必要があります。
しかし、MPM においては、物質に一定以上の負荷がかかると勝手に断裂を始めてしまうんです。たとえ千切れてほしくなくてもです。これは見方によってはかなりの困りものになります。
繋がりが流動的
MPM においては、良くも悪くも粒子同士の繋がりは非常に流動的です。
例えば、通常粒子法でゼリーを計算したければ、まず粒子の配置を行い、続いて初期状態で近接している粒子間に何らかのバネモデルを入れ、各計算ステップではバネに対して計算を行いますが、MPM ではそのような処理は不要です。初期状態で近くに存在している粒子があれば、それらは自動的に繋がりを持つのです。
これは、各粒子が変形勾配テンソルを独自に持ち、自身の変形具合を絶えず追跡することによって実現されています。
引き伸ばされた粒子は、自身の変形を元に戻そうと周りの空間(=セル)を引っ張ります。同じように引き伸ばされたすぐ隣にいる粒子も、同様にして周囲の空間を引っ張ります。すると、空間という媒介を通して、隣り合う粒子は互いに引き合うことになるのです。これが、隣接関係を陽に与えなくてもよい理由です。
物質が千切れてしまう理由もここにあります。弾性体が非常に大きく引き伸ばされると、本来はすぐ隣にいたはずの粒子が遠くに行ってしまうことになります。すると、それぞれが引っ張る空間同士に重なりがなくなり、それぞれの粒子は互いの存在を認識できなくなってしまうのです。こうして断裂が発生します。
一方、繋がりが流動的であることの利点として、自己衝突が自動的に計算できる点が挙げられます。にわかには信じがたいかもしれませんが、作成したシミュレーションには衝突検出の処理を一切入れていません。繋がりが流動的であるがゆえ、近づいた粒子間には自動的に繋がりが形成され、空間を通して互いを押し返す力が生じます。
しかし、外力などによって粒子同士が近付きすぎてしまうと、逆に強い繋がりが生じてしまい、粒子同士がくっつくことになります。これもまた難しい点です。
形状を記憶しない
初期状態の情報を与えなくてよいということは、裏を返せば初期状態を記憶することができないということになります。
ある瞬間における物質の(あるべき)形状は粒子の配置と各粒子の変形勾配テンソルによって決定されます。そして、それらは時間積分によって逐次更新されていきます。
もう分かりますね? そうです、誤差が蓄積していきます。
最初は配置が綺麗だったゼリーも、ブルンブルンと振動を繰り返すうちにだんだんと計算誤差が蓄積していき形が崩れ、最終的にはボロ雑巾も同然の姿へと化けていきます。しかも、繋がりが流動的であるがゆえ、自身の形が崩れていることを検知できません。
つまり、長期的に形状が保存してほしい場面においては MPM は不適ということになります。
ゼリーのキャラクターを主人公にしたゲームを作る……といった場合に MPM を採用すると悲惨な目に遭うことになります。
流体向け?
以上の難点は、流体シミュレーションにおいては問題になることがありません。通常の粒子法で必要だった近傍粒子探索が必要なく、より高速な計算が可能になる MLS-MPM は今後流体表現でリアルタイム計算に活用されていくのではと思います。
……と言いたいところなのですが、流体計算に使おうとするとそれはそれで難しい問題が生じてきます。
この辺りの話はまた改めてしたいと思います。
-
つい MPM 法と書きたくなるんですが、最後の M が Method なので MPM 法では redundant です。
高速 FFT 変換みたいな。↩︎ - 本当は物好きな人を集めてゼミとか開いて輪講したかったんですが、筆者の時間と物好きな人の数が足りませんでした。 ↩︎
- CUDA くらいまで自由度が上がると楽なんですけどね。シェーダだとかなり厳しいです。不可能ではないですが。 ↩︎
- 本当は単なる MPM ではなく MLS-MPM です。 ↩︎
- 複数の格子の境界上に存在する場合は、適当に好きな方を選んでかまいません ↩︎
- 運動量は保存します ↩︎
- 個人的にはこの移流方式自体を PIC 法と呼んでしまうのはやや違和感がありますが…… ↩︎
- SPH 法でも空間微分を行う際はカーネルごと微分しますが、それと同じです ↩︎
- 実際に書き込み可能な要素数の上限は環境に依存しますが、WebGL 2.0 は少なくとも 64 要素以上の書き込みができることを仕様で定めています。逆にそれ以上は期待しない方が無難です。インターリーブ方式にしない場合は、attribute 4 つ分(最大 16 要素)の出力までしか保証されません。 ↩︎