概念の左右と難しさ

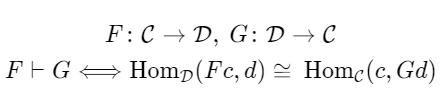
数学に関するポエム的な記事です。特に技術的な内容ではありません。圏論の知識があると共感が得やすいと思いますが読むために必須ではありません。

定義は詳細に説明しませんし数学的に厳密な話でもありませんが、明らかに間違ったことを書くつもりもないので、どこかが明らかに間違っていたら指摘してくれると助かります。

追記: 極限の左右を間違えていたので修正しました

随伴と逆

数学をやっていると随伴という概念に遭遇します。随伴というのは逆を緩めた概念です。

逆関数

逆関数を例に逆という概念と性質について説明します。分かっている方は読み飛ばして大丈夫です。

随伴という概念には遭遇していなくても、逆という概念に遭遇した方は多いと思います。例えば関数 f\colon\mathbb{R}\to\mathbb{R} に対する逆関数 f^{-1}\colon\mathbb{R}\to\mathbb{R} です。関数 f というのは何か実数 x（実数が分からない方は単純に小数以下を含む「数」だと思ってください）を受け取ったら、受け取った値に応じた実数 f(x) を返すようなデータのことです。逆関数 f^{-1} というのは、f の効果を完全に打ち消すような関数のことです。つまり、f を通した x の値 f(x) を再び f^{-1} に通すと、それは元の値 x と常に等しくなる f^{-1}(f(x))=x ということです。

ですが、f に対して f^{-1} が存在する条件というのは結構厳しいです。というのも、f が少しでも情報を潰してしまうとその効果を打ち消すことができなくなってしまうからです。例えば、「何かに 0 を掛けたところ、結果は 0 になりました。元の数は何でしょうか？」という問いは 0 を掛ける行為が情報を潰す行為に相当するので答えようがありません。逆（すなわち 0 で割る行為）が存在しないのです^[1]。

さて、関数 f の逆が関数 g だったとします。つまり、f は g によって完全に打ち消され、g は逆に f によって完全に打ち消されます。このとき、f と g は「完全に対等な関係」にあります。両者は互いのことを「自身の逆」として参照することができます。そこに立場の違いはありません。

随伴関手対

上では f と g を関数としましたが、以降は関手 F と G に置き換えて考えます。関手の説明を書くと長くなりすぎるので知らない方は関数みたいな何かだと思ってください。

関手についても前項のように逆を考えることはできるのですが、関手にしたことによって随伴という関係を考えることができるようになります。F と G が随伴の関係にあるとき、両者には左と右という立場の違いが発生します。随伴は、本来互いに逆にはならないような関手の対 F と G に対しても対を結成することを可能にします。その代償として、F と G にはそれぞれ完全に対等な関係ではなく、左と右という立場の違いを要求します。F が G の左随伴である（すなわち、G が F の右随伴である）ことを F\dashv G と表記します。このとき F と G は随伴関手対と呼ばれます。

さて、こうして制約を緩めたことによって、右と左という立場の違いが生まれてしまった一方で、随伴という概念を今までより多くの対象に適用することが可能になります。

というか、実は任意の概念が随伴になります^[2]。

随伴関手対の性質

関手 F と G が随伴になっている（F\dashv G）とします。このとき、F と G は互いに「鏡写しのような関係」になっていると言えます。一見すると全く異なる振る舞いをする2つの関手が、随伴という「鏡」を通して驚くほど綺麗な対称性をもって結ばれます。

さらに、ある関手の左（あるいは右）随伴は、存在すれば一意であることが示されます。ここから分かるのは、随伴という関係は関手の部分的な性質を定めるのではなく、極めて強固な制約をもって2つの関手の間の関係を完全に記述するものであるということです。

F と G が随伴関手対になっていれば、片方の関手の情報が消されたとしてももう片方の関手から完全かつ一意的に^[3]復元することができます。F と G は互いに互いを特定するための必要十分な情報量を持っていることになります。

つまり、F と G の持つ複雑さは本質的に同じであるということができます。

---

余談: 極限と随伴の関係

圏論を知っていて極限と随伴の関係を忘れてしまった人（例：自分）向けのメモです。そうでない方は読み飛ばしてください。

• 図式とは添え字圏 J から圏 C への関手 J\to C（すなわち関手圏 C^J の対象）のことである
• 対角関手 \Delta\colon C\to C^J とは C の対象 a を定数関手 \Delta(a)\in C^J に当てはめるような関手のことである
• 図式 T\in C^J の極限とは \Delta から T への普遍射のことである
• 図式 T\in C^J の余極限とは T から \Delta への普遍射のことである
• 任意の J 型の図式について極限（余極限）が存在する場合、図式を極限（余極限）に写す極限（余極限）関手 \operatorname{lim}（\operatorname{colim}）\colon C^J\to Cが存在し対角関手の右（左）随伴となる
• すなわち極限・余極限関手と対角関手の間には次のような関係がある: \operatorname{colim}\dashv\Delta\dashv\operatorname{lim}
• \operatorname{lim} は \lim\limits_\gets、\operatorname{colim} は \lim\limits_\to と書かれることがあるが、矢印の向きは随伴の左右と逆である

概念の左右

さて本題です。任意の概念が随伴になると書いたように、数学におけるあらゆる概念について背後に潜む随伴関手対を見出すことができます。随伴には左右という概念があるので、結果としてあらゆる概念に左右という概念が付いて回ります。

ただし、左右というのはあくまで一対の随伴関手対における関係なので、ある関手が「左」であると同時に「右」である、ということも起こり得ます（F\dashv G\dashv H の G など）。一方でそういった例はそこまで多くないので、多くの概念に左右を当てはめることができるのも事実です。

以下では誰でも知っている簡単なものからやや難しいものまで概念の左右の例を挙げていきます。ペアになっているものは直接随伴であるか、さもなくば随伴関手列で接続されています（つまり「情報量が同じ」です）。

0 と 1

誰でも知っていますが、誰でも知っていることはその概念が単純であることを意味しません。実際これらは非常に興味深い数学的対象です。0 と 1 と言っても色々ありますが、ここでは自然数（すなわちモノの個数）としての 0 と 1 を考えます。このとき 0 は左側、1 は右側の概念になります。具体的には \text{Set} における空図式の余極限と極限が 0 と 1（始対象と終対象、空集合と1元集合）です。

（集合の）直和と直積

名前はややこしいですが概念は誰にでもわかります。何か物が入っている袋が2つある状況を想像してください。このとき「一度1つの袋に中身をまとめてから一つ取り出す」のが直和、「2つの袋に同時に手を突っ込んで一つずつ取り出す」のが直積に対応します^[4]。直和が左側、直積が右側の概念になります。具体的には \text{Set} における離散2点圏 \{*\ *\} を添え字とする図式の余極限と極限が直和と直積です。集合の場合は直和の代わりに非交和と呼ばれることもあります。

自由構成と忘却

忘却というのは「何らかの付加的な数学的構造を忘れる」ことを意味します。例えばリンゴは食べ物ですが、「食べ物である」という性質を忘れることによってただの「物質」として扱うことが可能になります。このように忘却というのは「情報を失う」行為です。ですから一般に逆というのは存在しえません。しかし、逆を緩めた随伴という形であれば忘却のある意味での「逆」を考えることができます。それが自由構成です。忘却は右、自由構成は左の概念になります。

忘却の逆が考えられない理由は、候補が一意に定まらないからです。元々覚えていた情報が何だったか特定することができないため、どの情報を思い出すべきか決めることができないのです。逆に言えば、どの情報を思い出すべきか適切に決めることができるなら忘却の「逆」を定めることができるのです。

自由構成では、あらゆる状況において考えられる無数の復元可能性のうちから最も適切なものを一つ選択する方針を提供します。考えられる可能性のうちから最も「自由」であるものを選ぶことによって、情報が失われた状態から付加情報を一意的に構成するのです（もちろん失われた情報を復元することはできないので、忘却してから自由構成をしても一般に元通りにはなりません）。

商と部分

「何かの部分を抜き出すこと」は「同値関係による商」と対応します。例えば「整数全体から 12 の倍数を抜き出す行為」を考えてみましょう。これは部分です。結果として 12 の倍数が得られます。これに対応する行為は「整数全体のうち 12 の倍数を全て同一視する行為」になります。同一視するというのは「同じものとして扱う」という意味です。結果として 12 で割った余りが得られます。時計を想像してください。12時＝0時です。これが商です。商が左、部分が右に対応します。

余核と核

零対象と呼ばれる特別な役割を果たす存在があるとき、核と余核という概念が定義されます。写像 f\colon A\to B の核とは「f によって 0 に潰されるような A の部分」のことです。一方余核とは「f の像（＝ A 全体を f で写したときに得られる B の部分）による B の商」のことです。分かりにくいので言い換えると、「f の像全体がちょうど 0 に潰れるように B を潰したときに残る空間」のことです。このとき余核が左、核が右に対応します。

直積と冪

関数のカリー化と深い関係があります。直積 A\times B を受け取って C を返す関数は、A を受け取って「B を受け取って C を返す関数」を返す関数と同一視できます。「B を受け取って C を返す関数」というのは冪 C^B であると考えることができます。「直積で B を付与する行為」が左、「B 乗する行為」が右に対応します。

テンソル積と Hom 関手

もはや簡単な説明が不可能なので書きませんが、テンソル積が左、Hom 関手が右に対応します。

概念の左右と難しさ

ここまでいくつか概念のペアとその左右を見てきました。ここで面白い発見があります^[5]。それは「左に出てくる概念が右に出てくる概念よりも人間にとって“難しい”ことが多い」というものです。

0 と 1

人類にとって 0 という概念は 1 よりもずっと難しいものでした。何かが存在することを認識することよりも、「そこに何もない」こと、すなわち無を認識し、それを有（すなわち1以上の数）と同列に扱うことに成功したのは、人類が数という概念を扱い始めてからずっと後のことです。

直和と直積

集合論に限らず代数学、幾何学など様々な分野において直積とは一貫して「ペアを取る操作」「組を作る操作」として直感的に解釈できます。一方で、直積の左に対応する概念である直和（＝余直積）は舞台によって様々に姿を変え、時には直積と同じように振る舞い、時には定義のために複雑な構成をさえ必要とします。

特に、群論においては一般に「直和」と呼ばれているものと「直積の双対という意味での直和（＝余直積）」が異なります。群論において直和は直積とほとんど同じように振る舞いますが、余直積は「自由積」と呼ばれる全く別の概念に対応します。

---

余談: 直和が姿を変える理由

舞台によらず直積が一貫して「ペアを取る操作」であるのに対して、直和が一貫した姿を持たないのは実は圏論的に説明が付きます。付加的な構造を剥がす忘却関手は自由関手の右随伴であり、右随伴関手は極限を保存するという性質があります。直積は極限なので、直積を取る操作と構造を忘却する操作は可換になります。したがって、集合の上にどのような数学的構造が付加されているかに関わらず、直積を取る操作というのは「集合として見たときにペアを取る操作」であることが保証されているのです。

一方で、忘却関手が右に随伴関手を持つことは稀であるため（例外として位相空間の圏などが該当します）、一般的には忘却関手は余極限、特に直和を保存しません。したがって「集合として見たときに同じ操作である」という保証は全くなく、舞台が変わればその姿を変えるのも不思議ではないということになります。

---

自由構成と忘却

構造を捨て去ることは簡単です。しかし、存在したかもしれない構造の中から適切なものを探し出し再構築する作業はそこまで簡単でないことが多く、概念的にも自由構成は忘却に比べ（この場で簡潔に説明することが不可能な程度には）難しいです。自由構成を行う関手である自由関手は忘却関手の左随伴として定義されます。

商と部分

「商」という概念と「部分」という概念を比較したとき、大多数の人は「商」という概念の方にとっつきにくさを感じるのではないでしょうか。実際、「商集合」という概念が「部分集合」という概念よりも難しいものであるという意見に異を唱える人はほとんどいないのではないかと思います。

普通の理系の学生であれば「ベクトル空間の部分空間」という概念を知らない人はほぼいないでしょうが、「ベクトル空間の商空間」まで把握している人はさほど多くないはずです。恐らく多くの大学では（数学科でもない限り）線形代数のカリキュラムに商空間は入ってすらいないのではないでしょうか。同様に、位相空間論においても部分位相は確実に教科書に載っているであろう概念であるのに対し、商位相は教科書によって載っていたり載っていなかったりします。

しかし、随伴の章で説明したように、これらの概念は随伴関手を通して接続されている、すなわち本質的には全く同じ数学的な複雑さを持つのです。にもかかわらず、商と部分という二つの側面が人間に与える複雑さの印象は大きく異なります。

余核と核

これも同様です。核はカーネルとも呼ばれ、こと線形代数学においては手足のように使われる当たり前の概念ですが、双対である余核に光が当たることはあまりありません。

加群やホモロジー代数といった分野では余核も活躍を見せますが、これらは通常は数学科生でもなければ深く触れることはない分野です。

テンソル積と Hom 関手

これも、一般にはテンソル積の方が難解な概念として知られているのではないでしょうか。Hom 関手の方は名前こそあまり一般に知られていないかもしれませんが、基本的に「2つの対象を結ぶ射を全て取ってくる」というだけであり、少なくとも Hom 関手という概念自体が難解であるわけではありません^[6]。

微妙な例

これまで「左側の方が難しい」と思われる例を見てきましたが、これは全てに当てはまるわけではなく、微妙な例、あるいは逆転しているのではないかとすら思える例もあります。

忘却関手の右随伴

通常忘却関手の左随伴が自由関手となりますが、位相空間の圏 \text{Top} などでは忘却関手の右随伴が存在します。これも自由構成の一種^[7]であり、\text{Top} の場合は集合に密着位相を入れること^[8]に相当します。こうなってしまうと忘却と自由構成の間に難しさの差がないということになってしまいそうです。

他にも全称量化子と存在量化子、完全グラフと辺が存在しないグラフなど、両極端な自明な構造が見られる場合に忘却関手の左右随伴が存在することが多いようです。確かに導入される構造が自明であるならば、構造を忘れることと大して難しさに差がないような気もしてきます。

直積と冪

A を直積で付与する関手 -\times A と A 乗する関手 -^A が左右の随伴になります。個人的には指数を考えるよりもペアを作る方が概念的に簡単なように思えてしまうのですが、直積の方が左側に来ています。

差が生まれる理由

理論上は全く同じ複雑さを持つ概念であるにもかかわらず、なぜ概念の左右によって理解の難易度に差が生じるのでしょうか。

これについての明確な答えはまだ得られていませんが、自分の中では「数学という営み自体」あるいは「人間の思考方法」に元来的な方向があり、それに逆行する概念は人間にとって理解し辛いのだろうというような理解に落ち着いています。

なにせ数学的には同じ複雑さであることが分かっているので、その答えは数学の「外」に求めるしかありません。あるいは、人間の思考や数学の方向を定式化して、それに基づいて数学の中で数学の難しさについて理論を組むというようなことがもしかしたらできるのかもしれません。

つくづく人間というのは不思議な生き物であると思います。