AHC031 参加記 & 1位解法解説

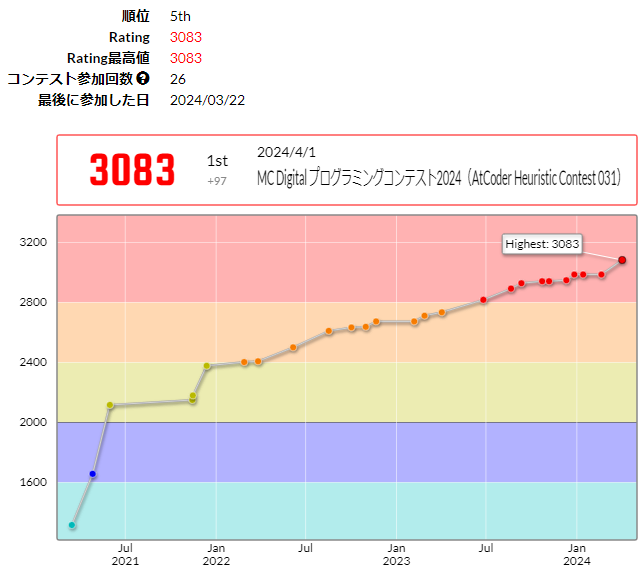
先日まで開催していた MC Digital プログラミングコンテスト2024 (AtCoder Heuristic Contest 031) でなんと優勝することができたので、自分の解法について途中の考察を交えつつ解説していこうと思います。

問題

詳しくは公式の問題ページを見てください。ざっくり説明すると

• 1000×1000 のマスでできたフィールドに、重ならないよう N 個の領域を割り当てる
  • 領域は長方形でなくてはならない
  • 領域が割り当てられないマスがあってもよい
  • これを 1 日として、全部で D 日分の割り当てを決める
• 各領域は要求される最低面積が決まっており（日ごとに変動）、下回ると特大ペナルティが発生する
• それぞれの領域は、長方形の外周をパーティションで囲われる
  • パーティションの厚みはゼロ
  • 各日において、必要十分なパーティションのみが設置される
• 日をまたぐ際のパーティションの設置・撤去の長さの合計がコストとなる
  • 初日の設置および最終日の撤去コストは無視できる
• コストが小さいほど点数が高くなる
  • 具体的には、全参加者のうちそのケースで出た最も小さいコストを C_\text{min}、自分のコストを C とすると、スコアは 10^9 \times C/C_\text{min} となる（相対評価）

という感じです。「初日の設置および最終日の撤去コストは無視できる」というのがかなり重要なポイントで、これにより初日から最終日まで設置しっぱなしの壁はコストが一切かからないことになります。

考察

細かいアルゴリズムはさておき、とりあえずどういうプランを立てると良さそうかというのを考えてみます。

まず、それぞれの日について各領域の要求を満たすことを考えます。これは、1000×1000 の正方形を適当な方法で N 個の長方形に分割し、分割された長方形に各領域を割り当てればよさそうです（ただし、長方形の面積が領域の要求を下回らないように注意する必要があります）。

コスト関数を考えると、d 日目と d+1 日目で使用するパーティションはできるだけ共通している方がよいということが分かります。つまり、領域の境目はできるだけ変化しない方が得ということになります。

ここで思い付くアプローチとして、木構造を使用するものがあります。1000×1000 の正方形を再帰的に縦または横に 2 分割することで各日の配置を決定し、できるだけ根に近い分割を各日で変化させないようにするというものです。

この方針はかなりよさそうに見えるのですが、明らかに実装が複雑になり、局所探索が難しくなるという難点があります。もう少し簡単な方法がないか考えてみます。

さて、木構造によるアプローチにおいて、あるノードにおいてどうしても分割の位置を（次の日に）変えなければならないとき、そのコストは分割に要するパーティションの長さに比例します。つまり、ノードの持つ空間（ここでは長方形です）を縦方向に分割する場合は長方形の幅が、横方向に分割する場合は長方形の高さが比例してコストにかかります。空間が正方形であるときは縦横どちらに区切っても変わりませんが、長方形が縦に長い場合は縦に分割する方が、長方形が横に長い場合は横に分割する方が得をするということになります。さらに、得をする程度は長方形が細長ければ細長いほど大きいということが分かります。

仮に、与えられている領域が 1000×1000 ではなく 1000000×1 であったとします。すると、長さ 1 のパーティションを N-1 個設置することにより、どのようなケースであっても一日あたりコスト N-1 以内のプランを組めることになります。これは明らかに最強です。

この事実から、1000×1000 の正方形を再帰的に木構造で分割するのではなく、最初にできるだけ細い領域（＝短冊）に分割してから、各短冊内の分割を考えるというアプローチに辿り着きます。今回のコンテストの最上位陣は、自分含め恐らく全員このアプローチであったと思います。以降は、この方針をベースに細かい部分を詰めていきます。

短冊への分割

短冊への分割に必要なパーティションの長さは (短冊の個数 – 1)×1000 と大きいので、できれば初日から最終日まで設置しっぱなし（＝コストゼロ）にしておきたいです。ある短冊への分割がある日で可能であるかどうかは、ビンパッキング問題を解くことで求まります^[1]。D 日間全てに渡って分割可能である短冊のうち、最も効率のよさそうなものを求めることが目的になります。

分割した後に短冊内の配置の最適化をしたいので、分割自体にはあまり時間をかけられません。最終的に次のような焼きなまし法によって分割を決定しました。

状態と近傍

和が 1000 になるような分割の幅を状態に持ちました。初期状態は分割なしの \{1000\} から始めて、以下の近傍で遷移を試みます。

細分化

幅をランダムに選び、ランダムに 2 つの幅に分割します。ただし、大きい幅のものほどよく選ばれるようにします。幅を大きい順にソートしておき、[0,1) の一様乱数を 10 乗してその割合の添え字にあるものを選ぶようにしました。

分配

幅をランダムに 2 つ選び、和が一定の条件で幅をランダムに分配します。

結合

幅をランダムに 2 つ選び、結合する……遷移を入れたような気がしたんですが、最終提出を見たら入っていませんでした。なんで？？

細分化 2

特殊な遷移として、分割がされていない状態 \{1000\} ではランダムに 6～9 個ほどへの分割を試みます。これは、空き容量が厳しい場合に、2つには分割できないがより細かい短冊であれば分割できることがある^[2]ためです。

コスト計算

各分割へのコストは毎回計算し直します。まず、どこか 1 日でも分割が不可能な場合（＝要求される面積を満たせない領域が発生する）はコストを \infty とします。全ての日に分割が可能な場合は、短冊内の壁を再利用しない前提にすると厳密なコストが簡単に出せるので、それを暫定コストとして焼きなましを行います。

ある日において分割が可能であるかの判定は、貪欲な初期配置を作成してからの 2 要素以内の交換と移動を繰り返してペナルティ（＝短冊をはみ出した高さの合計）がゼロにできるかで判定します。それぞれの日において要素数は高々 50 しかないので、貪欲な改善は十分高速に終了します。

分割の成功確率を上げる

ここが難しめのケースで非常に重要な点であったと思います。当然ですが貪欲な配置と改善では高々 50 要素といえども探索可能な範囲は狭く、結果として空き容量が小さい日において本当は分割可能なのに分割不可能と判定してしまうケースが頻発します。

さて、それぞれの日に分割が成功する（＝正しく分割可能と判断する）確率を p、分割が（本来可能なのに）不可能と判定してしまう確率を 1-p とします。全体で分割が成功するためには、全ての日程で連続して成功を引き続ける必要があります。つまり、日数を D とすると、成功確率は p^D になります。仮に反復を 100 回繰り返せるだけ時間があるとすると、そのうち 1 回でも分割が成功する確率は 1-(1-p^D)^{100} になります。p=0.8, D=30 を入れてみると、この値は 0.12 程度になります。つまり、100 回試したとしても分割が一度でも成功する確率は 1 割程度に留まります。

ここで試行の方法を変え、それぞれの日に 10 回ずつ分割を試し、一度も成功しなかった場合にのみ失敗するようにしたとします。すると、ある日に分割が成功する確率は p から 1-(1-p)^{10} へと変化します。したがって、D 日連続で成功する確率は (1-(1-p)^{10})^D になります。今度はそれぞれの日に 10 回ずつ試しているため、前よりも一度の試行に 10 倍の時間がかかり、同じ時間で分割を試せる回数は 100 回から 10 回に減少します。この 10 回のうち、分割が一度でも成功する確率は 1-(1-(1-(1-p)^{10})^D)^{10} になります。式が複雑になりましたが、先程と同じ p=0.8, D=30 を入れてみると、この値は 1 になります。正確には

0.9999999999999999999999999999999999999999999999999999999251476111\dots

になりますが、これは 100% 成功すると言って問題ないでしょう。

結果として、同じ時間をかけたにもかかわらず、分割の成功率は 12% から 100% に上昇しました。これはあまりにも大きな差です。

この結果を踏まえ、先程の貪欲判定にランダム性を加え、空き容量に依存して 1 回～4000 回^[3]の試行をそれぞれの日に行っています。

空き容量に応じて試行回数を変える理由は、空き容量が大きい場合に貪欲配置に失敗した場合、それは本当に分割が不可能である可能性が高く、同じ日に何度も試すメリットが薄いためです。

また、以下のような工夫を加えました。

難しい日から試す

焼きなましの過程において、多くの分割は本当に不可能です。このようなケースを早期に落とすため、空き容量が小さい、すなわち難しい日から順に分割を試みます。

不可能な分割を早期に発見する

上記に加え、反復試行を始める前に、それぞれの日において明らかに分割不可能な状態になっていないかを判定するロジックを入れています。これは、要素を大きい順に n 個選んで DFS で詰めていき、詰め込みが不可能であると分かった時点で探索を打ち切るものです。空き容量が多い日でもこの判定で落ちることがままあるので、上記の方法と組み合わせることで大きな効果を発揮します。

このような工夫の結果、seed=1 のような難しめのケースでは他の参加者よりも大幅に細かい分割を達成することができたと思います。

#AHC031 42.07B で暫定1位フィニッシュでした　2位が僅差すぎてシステス終了まで何も分からない…

2段階の焼きなましをしました
最初：全日程を短冊に分ける
以降：短冊内の配置をひたすら焼く

動画は seed=1 の様子 pic.twitter.com/Ldp9sRCuJ1

— さはら (@shr_pc) April 1, 2024

短冊内の配置の最適化

ここでも焼きなまし法を用いました。実行可能な状態（＝領域の最低面積を満たしている状態）をキープしながら配置を調整していきます。

状態

状態は、各要素の所属する短冊と、短冊内の位置としました。短冊内の要素は最小の高さを取っているものとすると、各要素の間にゼロ以上の隙間ができるので、その隙間のどこかに壁を配置するものとします。前後の日で隙間の共通部分が存在する場合は、そのどこかに壁を置くことで再利用することができるので、隙間同士の隣接する日へのリンクについても状態として持っておきます。

要素の配置・削除に伴い隙間が動いた場合は、リンクの有効性のチェックと貪欲なリンクの再構築を行います。それぞれの隙間の個数とリンク状態が分かれば、厳密なスコアを計算できるので、そのスコアを焼きなましに用います。

中間に貪欲なリンクの再構築が挟まるため、近傍に対するスコアの差分計算は困難になります。代わりに変更自体は軽量なため、全ての操作を可逆にして、遷移に失敗したら巻き戻すことで高速なスコア計算を可能にしています。

変更のログを記録するスタックを持っておき、

• 変更を巻き戻すのに必要なデータ
• 変更の種類

を変更が生じるごとにこの順に push します。巻き戻す際は、最初に変更の種類を pop し、種類に応じた分量の必要なデータをさらに pop して巻き戻しを行います。

近傍

次のような近傍を用いました。

区間短冊反転

短冊をランダムに 1 つ選び、また適当な日にちの区間を [0,D) の連続する部分集合から選び、その区間における選んだ短冊の上下を全てひっくり返します。区間内の壁の連結は保ちつつ、区間の端における連結性の変更が行われます。

短冊内シャッフル

短冊と日にちをランダムに 1 つずつ選び、その日における短冊の中身をランダムに再配置します。

短冊ミックス

短冊 2 つと日にち 1 つをランダムに選び、その日における 2 つの短冊の中身を交ぜて再分配します。

要素移動

短冊 2 つ (A, B) と日にち 1 つをランダムに選び、短冊 B から要素をランダムに選んで短冊 A 内に移動し、短冊 A をシャッフルします。

要素交換

短冊 2 つと日にち 1 つをランダムに選び、それぞれの短冊から要素を 1 つずつ選んで交換します。交換の結果、今周辺にある隙間で大きさの変化を吸収できなくなった場合は、短冊の中身をシャッフルします。

また、易しめのケースにおいて、しばらく更新がなかった際に短冊の幅を強制変更する kick 近傍を次のように設定しました。

短冊幅変更 kick

ランダムに短冊を 2 つ選び、幅を和から再分配します。対象となった短冊は、全ての日においてシャッフルします。

近傍割合の最適化

各近傍の割合は Optuna を用いて経過時間に対して線形変化するパラメータで決定しましたが、そもそも遷移試行回数が非常に大きかった (10^6～10^7 オーダー) からか、そこまで大きな効果はありませんでした。

時間の分配

以上のように、「短冊への分割」と「短冊内の配置の最適化」の大きな処理が 2 つあるわけですが、処理時間の大部分は後者に割かれています。具体的には、前者に 500 ms、後者に 2400 ms の時間を割り当てています。

ただし、空き容量が小さく分割がギリギリできそうでできないようなケース^[4]に対しては、2200 ms までの追加時間を割り当てます。これは、後半の焼きなましの時間が大幅に短くなったとしても、分割が成功して短冊に使う壁が共有できるだけで大きなコスト削減が見込まれるためです。

また、各日の空き容量はある程度ランダムに決まるため、特定のある一日のせいで分割が著しく困難になっているような場合には、その日を捨てる（＝短冊の分割対象から外す）ようにしています。捨てられた日は後から独立に分割が計算されます。どの程度の日まで捨てるかどうかの閾値は、時間が経過するほど低くしていきます。

最適解が達成可能なケース

全テストケース中に 1% 程度最適解が達成可能なケースが存在します。ここでの最適解というのは、パーティションを一切変更しないで全日程の要求が満たせるケースです。それぞれの日において n 番目に大きい要求の領域の最大値を a_n としたとき、a_1+a_2+\dots+a_N\leq1000^2 であれば最適解が達成できる見込み^[5]があります。

このようなケースでは、全参加者のうち少なくとも一人は最適解を出すであろうことが予想され、最適解が出た場合のコストは 1 になるため、最適解を出せなかった参加者のスコアは事実上ゼロになります。

そもそも全体の 1% 程度しかないというのもあり、このケースに対応するかどうかでそこまで大きなスコア差が付くものではありませんが、それでもこの対応の有無で順位が入れ替わるケースは大いにあったものと思います。

順位表から得られる情報

ちなみに、このようなケースの存在は順位表の情報から気付くことができました。

順位表を眺めていると、満点のちょうど 1/50 にあたる 1,000,000,000 点を獲得している参加者が数名見つかります。このようなスコアを 50 ケースの和で取ることは事実上不可能であり、かつ、複数人がこの点数を取っていたこと、これらの点を取った参加者のレートが特段高いわけではないことを考慮すると、

• 何か特殊なケースが存在し、そのようなケースについては容易に満点を取れるような方法が存在する
• その満点は、最上位のプレイヤーでも共有されている（それ以上伸ばしようがない）
• そのようなケースは、何らかの計算によって検出することが可能である（他を WA で落とさないとキリのいい点数は取れない）

ことが推測されます。これらの推測から、

• パーティションを一切動かさずに要求を満たせるケースが存在する

ことに気付くのは難しくないと思います。

結果と考察

暫定スコアでは終了時に 2 位とほぼ差がなかったんですが（スコア差 0.1%）、終了後のシステムテスト^[6]で差が付いて 1 位になりました。

何人かが結果を振り返るための統計情報を公開してくれています。ここでは自作のもの^[7]を使うことにします。こちらに見られるものがありますが、置き場所が暫定的なので将来リンクが変わるかもしれません。

上位 5 名のスコアを横軸を空き容量^[8]としてプロットした結果が以下のグラフです。

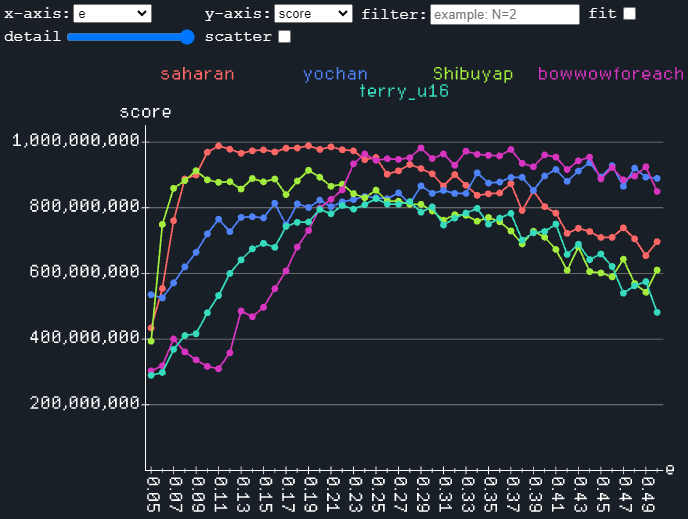
また、横軸を空き容量、縦軸を N（領域の個数）として勝率から色を塗ったものが以下の図です。

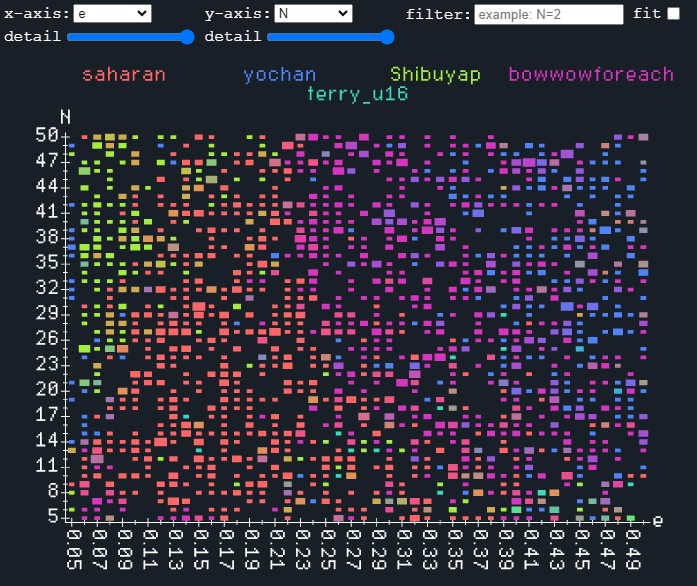
これから分かることは以下の通りです。

• 空き容量が少なめのケースで差が付いており、ここが得点源になった
  • 中でも N が小さいケースで有利であり、総じて難しめのケースに強かったと言える
• 一方で、空き容量が多めのケースでの成績は芳しくなかった
  • が、そこまで全体で差が付いているわけではなかったので、耐えた

空き容量が多めのケースであまり強くなかった理由としては、後半の焼きなましの近傍に短冊の幅の調整を（kick 以外に）入れていなかったことが原因ではないかと推測しています。全体に余裕があれば短冊の幅が調整できる可能性が高まるので、より良い局所に到達できたのではないかと思います。

おわりに

今回も面白い問題でした。問題を見た直後は「もしかして典型的な焼きなまし高速化バトルの問題かな？」と思ったのですが、実際に取り組んでみると予想以上に奥が深く、最後まで改良のアイデアを試し続けることができました。

実はコンテスト最終日の 4/1 は大学修了後の初出社日であり、業務中に学生 or 有給勢に抜かれないか気が気でなかったです（終了直前に一度抜かれました）。Twitter を見た感じ同じ境遇の人が他にもいてシンパシーを感じていました。今度からは調子のいいときは有給を取ろうと思います。

AtCoder Heuristic Contest は開始当初から 25 回以上参加してきましたが、rated なコンテストでの優勝は初めてなので非常に嬉しいです。ずっと目指していたレート 3000 の大台に乗るとともに、今年初めに一瞬で剥奪された金冠^[9]を再び被ることができてとても感慨深いです。

もはや上には全員優勝回数が 3 回ある猛者しかいないのですが、この位置をキープ＆あわよくば上に上がれるように頑張っていこうと思います。