AHC056 参加記 & 1位解法解説

最近参加していたプログラミングコンテストの HACK TO THE FUTURE 2026 （AtCoder Heuristic Contest 056） でなんとまた優勝することができたので、参加記と解法の解説を書いていきます。

最近コンテストの記事ばっかりになっていて恐縮なんですが、本当に楽しくてつい熱中してしまい……　これを見ている皆さんも興味があればぜひ！　Heuristic Contest の人口はもっともっと増えてほしいところです。

問題

2 次元のグリッド上を動くチューリングマシンを模したロボットがあるので、マシンの状態遷移関数とグリッド上の各マスの初期の色（＝読み書き可能なメモリの値）を決めて、与えられた目的地を順に訪れるようなマシンを設計します。

マシンの内部状態数と色数の和を最小化せよ、というシンプルな問題です。

詳しい説明は問題文のページを参照してください。

特筆すべき点としては、

マシンの動く経路は最短でなくてもよいが、テストケースごとに総ステップ数が 最短～最短の 2 倍 という制約があるので、これを満たす必要がある^[1]
グリッドにはランダムに壁が生えることがある。外周にも壁がある。壁に向かって一生直進し続けたりしないように注意が必要

あたりです。

考察

問題自体は至ってシンプルですが、とにかくこの問題が数学的に滅茶苦茶難しいことだけはすぐ分かります。チューリングマシンに関連する最適化問題は多くの場合 NP 困難にとどまらず計算不能にまでなるためです。

とはいえ、フィールドの大きさや最大ステップ数が制限されているため実際は計算不能とまではならず、別に最適解を求める必要もないので、いつも通り解法を考えていきます。

私の場合は初日は簡単に考えるために「色の書き換えをしない」という方針で解法を考えていたのですが……これが箸にも棒にもかからないというレベルでダメでした。

というのも、わりとコンテスト開始直後から同一スコアを取る集団がおり（以降団子と呼びます）、彼らがかなり強かったのですが、そのスコアに全くもって及ばなかったためです。

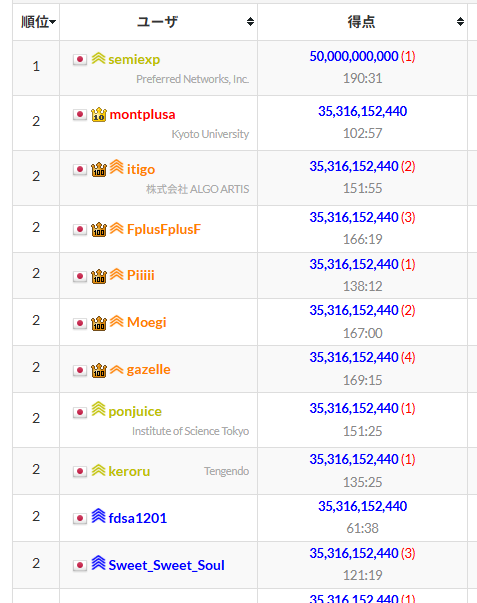
さすがにこの光景は AHC 史上初なのでは

というわけでなかなか大きなショックを受けつつ、まずは団子に到達するための方針を考えていたのが最初の土日あたりでした。

団子解法については既にいろんな人が言及しているはずなので、ここでは割愛します。ざっくり言うと「最短パスそれぞれ 1 手につき色と状態のペアを重複なく割り当てて、概ね $2\sqrt X$ （ $X$ は最短パスの移動回数）を達成する」というものです。

団子解法について考えていたこと

分かりやすい貪欲解法がある場合は、コンテスト中に同じスコアが出現すること自体はまあまあよくあります。特に短期だとよく見る光景です。

しかし、今回は時間が経ってもそこから抜け出す人が少ないところに異様さを感じていました。

大体の場合、思い付きやすい貪欲解法というのは、そこからある程度分かりやすい改善が存在します。つまり、一度はスコアが固まるものの、最終的にはみんなそこから大なり小なりの改善を経て脱出していきます。

しかし、今回は団子スコアを得ている人数が明らかに異常でした。したがって、団子解はある種の局所最適解になっており、そこから抜け出すためには本質的なアイデアの改善が必要で、それがなかなか難しいのでは？　などの考察をしていました。

結果的にこれは合っていたと思います。団子解法から抜け出すためにはルールの再利用が必須になります。

団子解法からの改善

やたら時間はかかりましたが団子解法に辿り着いたあと、そこからの改善を考えていました。

市松模様解法

途中で以下のツイートと全く同じ市松模様解法を思い付きました。

今回のAHCの比較的おもしろ構築？
最短経路長がXのときだいたいsqrt(2X)のスコアが出せる pic.twitter.com/2fLYN0nSAu

— _____ (@rho__o) November 17, 2025

グリッドを市松模様に塗ると、塗られたマスとそうでないマスを必ず 1 手置きに通ることになります。

そこで、2 手分の移動を一度に処理することを考えます。団子解法では色と状態のペアは各ステップにおいて任意に選ぶことができるので、どの状態を割り当てたかに「1 手後の移動方向」の情報を込めてしまい、市松模様の部分は同じ色で塗り潰してしまいます。

すると、状態方向について 4 回改行する必要があるので、団子解法ほど隙間なく状態と色のペアを詰めることはできなくなりますが、大体考えるべきパス長が半分になるので約 $2\times\sqrt{X/2}=\sqrt{2X}$ のスコアを達成できます。

市松模様解法からの改善

次に、市松模様解法で同色で塗る範囲をさらに拡大できないかを考えました。

これ以上同じ色で塗ると、周期性が崩れて事前に考えたパス通りに動けなくなる可能性が出てくるのですが、逆に最短経路で動かなくてよいのであればもっと同色で塗るマスを増やせるはずです。

同色で塗られた床が増えると、それらの床の上では曲がることができなくなり、止まれる床の上に到達するまで直進することになります。ここから氷の床解法の着想を得ます。

氷の床解法

フィールドを氷の床と停止床であらかじめ塗っておき、停止床を経由して氷の床を滑りながら目的地を経由する方針です。

思い付いてしまえば実装は比較的シンプルなのですが、特筆すべき事項として、

氷の床に向かって踏み出す方向と滑り出す方向を独立に設定できる

というものがあります。これによって、ある停止床からの行動パターンが最大で 4 通りから 16 通りにまで増えます。

ネックになるのがスコア計算で、目的地は最大で $N^2$ にまで膨らむので、毎回 Dijkstra 法などを走らせていたのでは遅すぎて局所探索ができません。そこで、停止床のみを頂点とするグラフ上の各頂点間に対する最短距離を事前に効率的な方法で求めておき、それを利用して $O(1)$ で各目的地に対するパスを構築することにしました。

辺の重みが 1 のみ、かつ全ての頂点からの距離を求めたいので、SIMD とビット並列による高速化が刺さりそうです。この辺りの高速化は ChatGPT が強いのを知っていたので、要件を指定しつつ方針を相談しながら実装を丸投げします。

書いてくれました。（一部抜粋）

...
// (AVX2) ------------
alignas(32) static __m256i V255 = _mm256_set1_epi8((char) 0xFF);
alignas(32) static __m256i BIAS = _mm256_set1_epi8((char) 0x80); // for unsigned comparison

// Work buffers (static)
alignas(32) static __m256i W[MAX_VS]; // per-vertex lane weights (8bit saturating)
alignas(32) static int
    Pred[MAX_VS][SIMD_LANES]; // per-vertex per-lane predecessor (used only when compute_prev==true)
alignas(32) static __m256i maskVec[MAX_VS + 1][MAX_VS]; // [level][v] 32-byte masks
alignas(32) static int U_level[MAX_VS][MAX_VS]; // vertex lists per level
alignas(32) static int U_count[MAX_VS];
alignas(32) static int distBatch[SIMD_LANES][MAX_VS];

// Epoch array to track whether a mask/level has been built for this batch
alignas(32) static int tagLV[MAX_VS + 1][MAX_VS]; // [level][v] last batch ID
static int batchEpoch = 1; // 0 is unused

// Precomputed vectors where exactly one byte is 0xFF for each lane
alignas(32) static __m256i BYTE_MASK[32];
static bool byteMaskInited = false;
if (!byteMaskInited) {
    rep0(i, 32) {
        alignas(32) uint8_t tmp[32] = {};
        tmp[i] = 0xFF;
        BYTE_MASK[i] = _mm256_load_si256(reinterpret_cast<const __m256i*>(tmp));
    }
    byteMaskInited = true;
}

for (int base = 0; base < numV; base += SIMD_LANES, batchEpoch++) {
    const int lanes = std::min(SIMD_LANES, numV - base);
    if (batchEpoch == 0) { // wrap-around protection (unlikely but safe)
        std::fill(&tagLV[0][0], &tagLV[0][0] + (MAX_VS + 1) * MAX_VS, 0);
        batchEpoch = 1;
    }

    int maxLevel = 0;
    rep0(i, lanes) {
        int s = base + i;
        rep0(v, numV) {
            int dv = distMat[s][v];
            distBatch[i][v] = dv;
            if (dv < INF)
                maxLevel = std::max(maxLevel, dv);
        }
    }
    ...

一部手直ししてますが、大体そのままです。これを自分で調べて書いていたらなかなか大変だったと思うのでありがたいです。

DP による経路復元

さて、氷の床を導入したことで面倒なことが一つ増えます。それは、目的地が氷の床の上にあった場合、どの方向から進入するかで次の初期位置が変わるという点です。

そのため、経路を探索するとき、各目的地に対して最大で 4 通り^[2]のパスを探索しなければならず、ここでもグラフの頂点間の最短経路の事前計算が効いてきます。

各目的地について個別にパスと最短距離を計算したら、先頭から DP で全体の最短路を求めることができます。

こうしてそれなりに高速にフィールドの構成 → スコアを求めることができるようになったので、適当に焼いて氷の床と停止床の配置を決めます。

これで中盤あたりに結構良いスコアが出るようになったのですが、それでも当時 10 位前後であり、最上位勢にはまだ大きな差を付けられていました。

最終解法（前半）

最終的な解法は、氷の床解法に反射板を足したものになります。なぜ反射板を追加しようと思ったかというと、

ターン数の制約が緩いケースでは、ターン数を使い切れていなかった
頻繁に通る曲がり角で必ず停止床を設置する必要があった

辺りの考察によるものです。

特に、今回は（普通の氷の床パズルとは違って）ルール上壁に向かって直進してしまうと、その場で止まることができず、永遠に直進してそのままゲームオーバーになってしまうので、与えられたターン数を使い切るより先に infeasible になってしまうという問題がありました。これは勿体ないですね。

また、例えば四隅で曲がるときなどは、進入方向に対して出る向きが完全に固定されているにもかかわらず、毎回違う色と状態のペアを割り当てているという状態になっていました。これも勿体ないので一色に圧縮したいところです。

反射板のイメージはこんな感じです。

挙動はシンプルなのですが……実は考えないといけないことが倍増して実装はとても大変でした。

反射板による困難

最も大きな問題として、各方向に滑る状態が均等に分散している必要があるというものがあります。

例えば、最終的に 7 状態があり、各状態に対する氷の床上での移動方向が以下のようになっていたとします。

0: →
1: →
2: →
3: →
4: ←
5: ↑
6: ↓

この状態で、→ を ↑ に変化させる反射板を通ることを考えると、反射板を通過後は、状態 0～3 が全て状態 5 に圧縮されることになってしまいます。使える色の数は決まっているので、反射前の情報の大部分が失われてしまうことになります。これは困ります。

というわけで、反射板による状態の変化は、ある種の単射性を保つ必要が生じます。

そのためには、まずは停止床に進入する方向（反射板があるため滑り出す方向とは必ずしも一致しないことに注意）が 4 方向に均等にばらけている必要があります。床を決定するときに、焼きなましの評価関数に進入方向の分散具合を組み込んだところ、若干効率を犠牲にしつつも大体のケースで ±10~20% 程度に回数の差が収まってくれました。

また、同じ方向に割り当てられた状態の中でも、反射後に区別しなくてもよい（＝状態が潰れてもよい）ものもある（例えば、反射板を利用せずに到着するような状態群は対応が多対一になっていてもよい）うえ、反射板自体が 2 種類あり、異なる変換ルールを割り当てられるため、これらを加味しつつ「本当に区別しなければならない状態群」に限って単射になるように反射板の写像を構成することで、ほぼ確実に状態が潰れないような変換ルールを構築することができました。

焼きなまし法で盤面と経路を決定する

最終的に利用した焼きなまし法は以下のようになりました。

まず、下準備として氷の床を市松模様に割り当てて全体の経路を構築し、最も多く訪れた停止床から貪欲に氷の床への変更を試みます。

これ以上減らせなくなったところで焼きなましを開始します^[3]。

状態遷移は

20%: ランダムに氷の床でないマスを選んで氷の床に変更
40%: ランダムに氷の床でないマスを選んで、隣接するマスのうち移動可能なものからランダムに選んで交換
40%: ランダムなマスを選んで、違う種類のマスに変更（氷の床へは変更しない）
- ただし、半分の確率で氷の床から選ぶ

という風にしました。この辺は時間がなかったのもありあまりガチガチに最適化していないので、時間経過で割合を変えるなどすればもうちょっと伸びる気がします。

平均的なケースでは手元で 6 万回くらい反復が回っていたような記憶がありますが、極端に遅いケースでは 1 万回回らないようなものもありました。

ここまでで、土曜日辺りに 5~10 位くらいを取っていました。まだ状態圧縮はしておらず、後半は団子解法と一緒です。

ここからどの程度圧縮できるかかなり未知数だったのですが、1 位までまだ結構な差が開いており、かつ今後大きく伸ばせる可能性のある方法が状態圧縮しか思い浮かばなかったので、圧縮可能な状態（と色のペア）の条件を紙に書いて方針を考えていきました。

最終解法（後半）

最終日からはひたすら状態圧縮のコードを書いていましたが、ロジックが本当に複雑で何度も頭が爆発しかけました。

条件の整理

状態圧縮に入る前に、色と状態のペアが満たすべき条件を整理します。

全体の経路のうち、停止床を訪れたところに「ユニーク状態」（ややこしいですが、マシンの状態とは別です）を割り当てていきます。一つのユニーク状態は、対応する状態と色、および動く方向^[4] $(c, q, d)$ を持ちます。このうち動く方向は、経路を決定した段階で確定するので、調整する余地はありません。全てのユニーク状態の色と状態 $(c, q)$ を決めると、自動的にルールが決定します。

時系列順に、ユニーク状態を $(c_1,q_1,d_1),\dots,(c_m,q_m,d_m)$ とします。滑る床から開始する場合は面倒なので一旦無視します。

また、各停止床の位置 $i$ について、位置 $i$ に対応するユニーク状態の添え字を、時系列順に $i_1,i_2,\dots,i_{m_i}$ とします。

特定の位置 $i$ にある停止床を考え、その上のユニーク状態 $i_k$ を考えます。このときの色と状態は $(c_{i_k},q_{i_k})$ で、動く向きは $d_{i_k}$ なので、次のようなルールが必要です。

(c_{i_k},q_{i_k})\to(?,?,d_{i_k})

$?$ の部分はそれぞれ書き換える色と移動後の状態が入ります。

書き換える色は、同じマスに対応する次のユニーク状態 $i_{k+1}$ の色 $c_{i_{k+1}}$ にすればよいので、

(c_{i_k},q_{i_k})\to(c_{i_{k+1}},?,d_{i_k})

と分かります。

では、移動後の状態は、時系列で次のユニーク状態 $i_k+1$ の状態 $q_{i_k+1}$ にすればいいかというと、反射板があるせいでそうはなりません。

2 種類ある反射板による状態変化の写像を $f_1,f_2\colon Q\to Q$ （ $Q$ は状態の集合）、ユニーク状態 $i$ から $i+1$ に至るまでに通過した反射板の種類を順に $r_{i_1},\dots,r_{i_m}$ として、反射板による状態変化の写像の合成 $f_{i+1}=f_{r_{i_m}}\circ\dots\circ f_{r_1}$ を定めたとき（反射板を通過していない場合は恒等写像とします）、逆像 $f^{-1}_{i+1}(q_{i_k+1})\subset Q$ の元のうち好きなものを $?$ に割り当てればよいです。

したがって、反射板の写像の構成と通った反射板の順序によっては複数の状態から選べる可能性があるのですが、あまりに複雑になるため、候補は 1 種類に固定してしまいます。この対応関係（欲しい状態 → 候補）は、反射板による状態変化の写像および全体の経路を決定した段階で、各ユニーク状態 $i$ に対して一意に定まるので、これを写像 $g_i\colon Q^\text{possible}_i\to Q$ としてしまいます。

ここで、 $Q^\text{possible}_i$ はユニーク状態 $i$ に到達する際に通過した反射板による状態変換の逆像が空にならないような状態の集合で、 $q_i\in Q^\text{possible}_i\subset Q$ を満たします。 $Q^\text{possible}_i\neq\varnothing$ は $f_1,f_2$ を構成するときに保証されるようにします。

すると、単に $?=g_{i_k+1}(q_{i_k+1})$ とすればよく、ルールは

(c_{i_k},q_{i_k})\to(c_{i_{k+1}},g_{i_k+1}(q_{i_k+1}),d_{i_k})

となります。

既にこの時点で十分ややこしいのですが、ここからさらにルールの圧縮をしていかなければなりません。ルールが圧縮できる条件は、2 つが完全に同一であること、すなわち、ユニーク状態 $i_k$ と $j_l$ のルールを圧縮したければ

c_{i_k} &= c_{j_l}\\
q_{i_k} &= q_{j_l}\\
d_{i_k} &= d_{j_l}\\
c_{i_{k+1}} &= c_{j_{l+1}}\\
g_{i_k+1}(q_{i_k+1}) &= g_{j_l+1}(q_{j_l+1})

をすべて満たす必要があります。

圧縮の方針

まず、全てのユニーク状態について、色は（氷の床と反射板に割り当てられているものを除いて）完全に自由に決められます。

また、状態についてもある程度自由に決められます。

状態 $q\in Q$ からその状態の滑り方向 $d\in\{U,D,L,R\}$ を決める写像を $f_\text{slip}$ とすると、各ユニーク状態 $i$ は特定の方向から滑り込む必要があるので、その方向を $d^\text{in}_i$ とすると、 $q_i$ は $f_\text{slip}(q_i)=d^\text{in}_i$ を満たす必要があります。

加えて、先程書いたように $q_i\in Q^\text{possible}_i$ も満たす必要があるので、最終的に $q_i\in f^{-1}_\text{slip}(d^\text{in}_i)\cap Q^\text{possible}_i$ が求められます。この右辺を $Q_i$ と定義します。これは事前計算で求めておきます。するとシンプルに、状態については $q_i\in Q_i$ という制約がかかることになります。

次に、ユニーク状態 $i_k$ と $j_l$ をマージした場合にどのような制約が発生するかを考えます。

c_{i_k} &= c_{j_l}\\
q_{i_k} &= q_{j_l}\\
d_{i_k} &= d_{j_l}

については単純ですが、さらに

c_{i_{k+1}} &= c_{j_{l+1}}\\
g_{i_k+1}(q_{i_k+1}) &= g_{j_l+1}(q_{j_l+1})

を満たす必要があり、これらが厄介な制約になります。

$c_{i_{k+1}} = c_{j_{l+1}}$ とは、すなわちユニーク状態 $i_{k+1}$ と $j_{l+1}$ に同じ色を割り当てなければならないことを示します。裏を返せば、これらのユニーク状態には同じ状態を割り当てることができません。

しかし、これは逆も成り立ち、これらのユニーク状態に違う状態が割り当てられていれば、条件を満たす色を後から割り当てることができます。したがって、 $c_{i_{k+1}} = c_{j_{l+1}}$ は $q_{i_{k+1}}\neq q_{j_{l+1}}$ と読み替えることができます。

ユニーク状態を多段階でマージする場合も、union-find のようなデータ構造で「同じ色が割り当てられているユニーク状態の集合」を管理すれば、同等の制約を実現できます。

こうすることで、ユニーク状態に陽に色を割り当てることなく状態圧縮を進めることができます。

陽に色を割り当てない最大のメリットは、状態の割り当てに対して常に最適な色の割り当てがされているまま処理を進められる点です。

焼きなまし法のテクニックで、2 つの状態を同時に焼く代わりに、片方のみを焼いて、もう片方を追従して（十分高速な方法で）最適に決めることで探索空間を小さくするというものがありますが、これに似ています。

残る制約

g_{i_k+1}(q_{i_k+1}) &= g_{j_l+1}(q_{j_l+1})

は状態に関するものなので、ユニーク状態に状態が割り当てられていれば管理が可能です。

しかし、それぞれ異なる写像の行き先が一致する、という制約を動的に扱うのは非常に複雑になるため、一度マージされたユニーク状態 $i_k$ と $j_l$ が存在する場合は、もう $q_{i_k+1}$ と $q_{j_l+1}$ の割り当ては固定してしまい、それ以上動かさない、ということにしてしまいました。

これはなかなか大きな枷ですが、状態圧縮の実装を始めた段階でコンテスト終了まで 24 時間を切っており、とにかく完成を急ぐ必要があったため、実装のシンプルさを優先することにしました。実際、これによって「リンクした大きさ 2 以上のユニーク状態の状態の swap をどう実装するか？」という面倒な問題を回避できた^[5]ので、良い判断だったと思っています。

さて、先程単純と書いた制約

c_{i_k} &= c_{j_l}\\
q_{i_k} &= q_{j_l}\\
d_{i_k} &= d_{j_l}

の中にも色を含むもの $c_{i_k} = c_{j_l}$ があり、これも状態の制約に還元する必要があります。これは、

ユニーク状態 $i_k$ と同じ色が割り当てられているユニーク状態の集合と
ユニーク状態 $j_l$ と同じ色が割り当てられているユニーク状態の集合

について、「ユニーク状態 $i_k$ と $j_l$ を除いて、同じ状態が割り当てられているようなユニーク状態のペアが存在しない」と言い換えることができます（ややこしい！）。

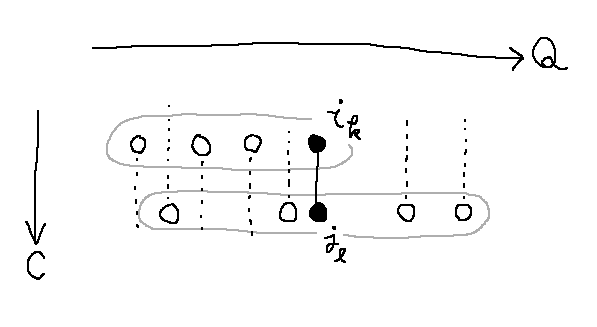
ややこしすぎるのでお気持ちの図を用意しました。白丸部分の状態方向の衝突がないというのが重要です。

状態の制約については、マージ後に「変化可能な状態の集合」を $Q_{i_k}\cap Q_{j_l}$ に設定することで、一度マージを行ったユニーク状態に割り当てる状態を安全に変更することができます。

これで「各ユニーク状態に割り振る状態」のみを変数としたまま、状態のマージを行えるようになりました。

山登りによる圧縮

最終的に、各ユニーク状態に割り振る状態をランダムに変更しながらマージ可能なユニーク状態をマージしていきます。

最終的には、使う色の数を最小化したいので、同じ状態が割り当てられているユニーク状態の個数の最大値を最小化したいです。そのため、以下のようなルールで状態の変更を行います。

ランダムにユニーク状態 2 つ $i,j$ を、 $q_i\neq q_j$ かつ $q_i\in Q_j$ かつ $q_j\in Q_i$ を満たすように選び、さらに同じ色に属するユニーク状態の集合上で状態の衝突が発生しないなら、 $q_i$ と $q_j$ を入れ替える
$n_q$ を、状態 $q$ が割り当てられているユニーク状態の個数とする。ランダムにユニーク状態 $i$ と状態 $q$ を、 $q_i\neq q$ かつ $q\in Q_i$ かつ $n_{q_i}\gt n_q$ を満たすように選び、状態の衝突が発生しないなら、 $q_i$ を $q$ に置き換える

さらに、ユニーク状態のマージは、 $n_q$ が最大値を取るような状態 $q$ を持つものに対してのみ行います。この制限が非常に強力でした。

当然ですがマージは行えば行うほど厳しくなっていくので、可能なものを次々マージしていくより、実際に最大値の改善に直結するもののみをマージすることで最大の効果が得られるようです。

また、状態圧縮を開始する際に使用する色数の初期値は決め打っておくのですが、圧縮によって色数が数割程度減ることを見越して、圧縮前に最適だった色数の 1.3 倍程度を割り当てることで、圧縮後の色と状態の図が正方形に近くなり、スコアが改善しました。

圧縮後の色の割り当て

状態圧縮によって、同じ色を取るべきユニーク状態の集合がたくさん得られます。これらを、積み木の要領で小さい数字の色から順に割り当てていきます。

運が悪いと空いた隙間によって最適な色数が達成されないことがありますが、後述する多スタートによってカバーします。

圧縮の多スタート

圧縮によるスコアの減少は、山登りを採用していることもあり、かなりバラつきがあります。

そこで、焼きなまし法によって得られた圧縮前の解がベストを更新する度にそれぞれの解について独立に圧縮作業を行い、最も良かったものを最終的な解とします。圧縮作業は高速に行えるので、それぞれの解に対して 10 ms を上限として圧縮を行いました。

最終結果

最終日にどうにか状態圧縮の実装を終えることができ、細かい部分を修正することで一気にスコアが伸びました。

！ pic.twitter.com/BA2fVCxmFa

— さはら (@shr_pc) November 17, 2025

さすがにここまで伸びるとは思っていなかったのでびっくりしました！　状態圧縮によってさらに 20% 近くスコアが改善したことになります。

最終的にシステムテストでも 2 位以下に大きな差をつけて優勝することができました。

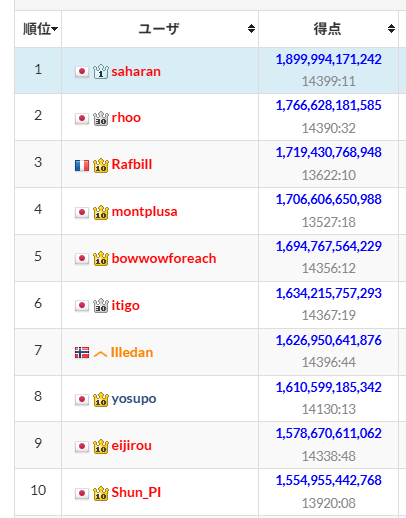
最上位勢の解法は、概ね氷の床 or ベルトコンベア方針と状態圧縮の組み合わせで、自分は状態圧縮の部分で特に大きな差が付いていたようです。

反射板を利用したのと、滑る方向を分散させるよう評価関数で調整したのが、圧縮パートでもうまく働いた可能性が高いのではないかなと思います。

世界一になりました

そして、今回の優勝の結果、なんと AtCoder の Heuristic 部門で Rating 世界一を獲得することができました！

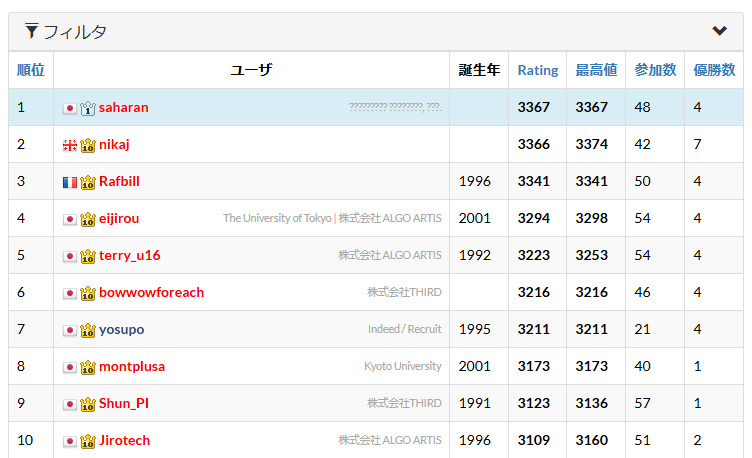
冠も金からプラチナに変化しています！

2 位くらいならいつか上振れて取れるかも……という期待はしていたんですが、まさか 1 位まで到達できるとは思っていなかったのでめちゃくちゃ嬉しいです。

とはいえ、2 位の nikaj とのレート差はわずか 1 なので、~~来月の~~（今月でした）短期コンテストで鉑冠が即座に剥奪される可能性は十分にあります。

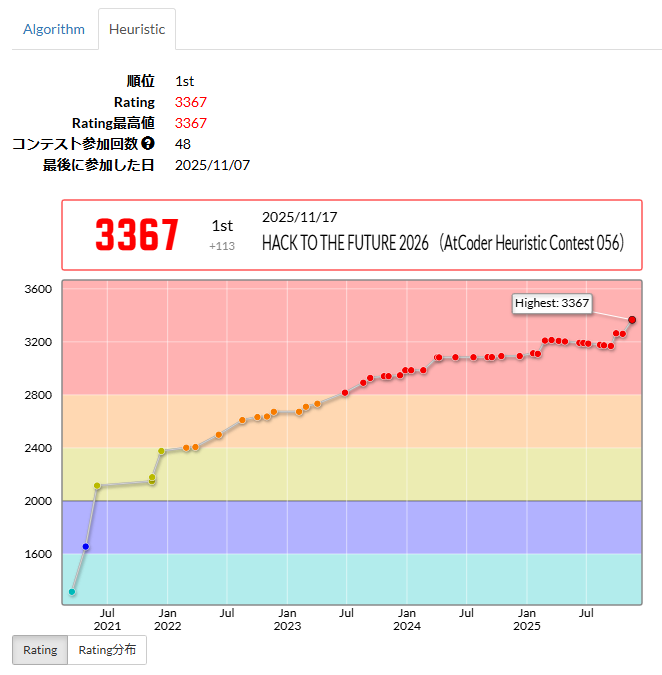
優勝した部分だけ露骨にレートが上がっているのが分かります。レートが 3100 を超えたあたりから top 3 くらいに入らないとまともにレートが伸びなくなるので、一気に伸びるか、じわじわ減り続けるかの厳しい戦いになってきますね。。

今の 1~4 位くらいのレート差であれば、長期（差によっては短期でも）で優勝した人に鉑冠がしばらく渡される、という流れになりそうです。

頑張ってこの位置を維持したいと思います！ 💪

X でも言及されていましたが、この制約が本当に絶妙で素晴らしいです。この辺りはひとえに作問者の wata さんのセンスだと思います。 ↩︎
内部的には停止 + 4 方向の 5 通りで処理しています ↩︎
できるだけ頂点数を減らしてからの方がたくさん反復が回るのでお得です。焼いてる最中にも停止床は減っていく傾向にあるので、焼けば焼くほどより高速に反復が回るようになるという不思議な特性を持ちます。 ↩︎
「動いた後滑り出す方向」とは独立なことに注意 ↩︎
真面目に考える場合、リンク後の大きさが $n$ のユニーク状態と swap する候補として、大きさの和が $n$ になるようなユニーク状態の集合を探してくる必要があります ↩︎