Sea of Papers: 解説

Sea of Papers の技術解説です。大量の紙切れが宙を漂いながら浮かんでいく様子を眺めます。以前の布とは違い、物理演算を GPGPU で行いました。スマホでも動きます。

大枠

物理演算

• 頂点座標と頂点速度を保存するテクスチャを用意する
• テクスチャ上の計 512×512 頂点を、8×8 頂点を一つのユニットにしてユニットを 64×64 個並べたものと見なす
• ユニット内に紙切れを再現するための拘束条件を仕込んで fragment shader で解く
• fragment shader で座標更新、外力計算を行う
• 外力用の流速ベクトル場を事前計算してテクスチャに焼き込む

描画

• vertex texture fetch で頂点座標が保存されたテクスチャから座標を読み込んで紙切れを表示
• volumetric lighting のために光っている部分をテクスチャに書き込む
• 光源を中心にして放射状にぼかす
• 加算合成でいい感じに合成する

詳しく見ていきます。

データ配置

GPU 上で計算を行うので、物理量は全てテクスチャに格納します。2冪のテクスチャだと効率が良い（正確には、効率が悪くならないことが保証されている）らしいので、512×512 のテクスチャにデータを格納することにしました。

少し前まで知らなかったんですが、最近のハードウェアだと2冪でないテクスチャも普通に使える^[1]みたいですね。WebGL でもサポートされていました。

今回は小さな紙切れをたくさん飛ばしたかったので、512×512 のテクスチャを縦横 64 分割して、8×8 テクセルのユニットが 64×64 個格納されているものと考えます。テクスチャは R, G, B, A と4チャンネルあり、空間は3次元なので位置と速度の6次元分の変数を格納するには2枚のテクスチャが必要になります。

物理計算における前提

真面目な物理シミュレーションでは、物理量の単位を国際単位系（SI）に合わせます。時間は秒、質量はキログラム、長さはメートル等々が基準になります。が、今回は物理現象を正確にシミュレートすることを目的としておらず、物理ベースアニメーションを作成することが目的なので、計算が簡単になる単位系を勝手に選びます。特に、時間の単位をフレームとし、時間刻み幅 \Delta t を 1 に選びます。したがって、以下の議論では時間刻み幅 \Delta t は完全に欠落します。ゲーム等に利用する場合でもこのような単位系で問題ないことが多いです^[2]。

長さ、質量については SI に従っていると考えても構いません。

テクスチャのデータ型

データ型の種類

物理シミュレーションを行うので、物理量に用いるデータはある程度の精度が必要になります。シミュレーションの内容に大きく依存しますが、大まかには

• byte 型 (8-bit int) は論外
• half float 型 (16-bit float) 型はかなり厳しい
• float 型 (32-bit float) 型は無問題

といった印象です。

byte 型で連続的な物理量を扱うのは無謀です。half float 型ではゼロ付近の数値は安定して扱えますが、少しでも絶対値が大きくなると途端に動きが離散的になります。また、計算によって保存されるべき量が丸め誤差によってどんどんズレていきます。

例えば今回のような計算では運動量が保存せず紙切れが原点周りを単振動しだし、Convection のような二層流計算では質量がみるみるうちに失われて空っぽになります。

スマホ対応における制約

以上のような理由から、可能であれば float 型を採用したいところです。が、残念なことに 2021 年になっても iOS の Safari が float 型のテクスチャをフルにサポートしていません！^[3]そのため、Android と iOS 両方のスマホで動かしたければ half float 型のテクスチャを使わざるを得ません。

WebGL での float 型テクスチャのサポートは複数の拡張に分けられており、

• OES_texture_float: float 型のテクスチャを作成可能にする
• OES_texture_float_linear: float 型のテクスチャに対して線形補間が使えるようにする
• WEBGL_color_buffer_float: float 型のテクスチャに書き込めるようにする

の3つが揃って初めてフルに使えるようになります。iOS では上二つの拡張はサポートしていますが、一番下の拡張だけサポートしていません。シェーダを通して計算結果をテクスチャに書き込んで更新するのがシミュレーションの流れなので、テクスチャに書き込めない時点で全く使えないも同然です。

執筆時点で WEBGL_color_buffer_float が標準で使えないのはもはや IE と iOS の Safari だけとなっており、時代に取り残されないよう早急に対応してほしいところです。

どうにかして half float 型を使う

計算上色々な問題が発生する half float 型テクスチャですが、計算を工夫することでどうにか対処できなくもありません。

Convection では、本来解く必要がない質量保存に関する方程式を定期的に解き、失われていく質量を補填する計算を行っています。

また、今回の計算では位置ベース物理にありがちな「前ステップの位置との差分から速度を算出する」方式を取らず、位置と速度を分離して計算・保存することでどうにか精度を保っています。

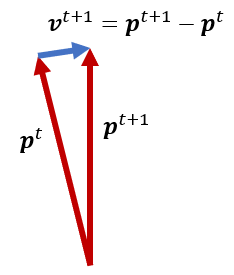
時刻 t+1 と時刻 t における位置ベクトルの差分 \bm p^{t+1}-\bm p^t から時刻 t+1 における速度ベクトル \bm v^{t+1} を算出する場合、上図のような計算が発生します。

赤いベクトルがテクスチャに保存されているベクトルで、青いベクトルが計算によって算出されるベクトルです。

浮動小数点数は絶対値が大きくなるほど精度が落ちるので、\bm p^{t+1} と \bm p^t の精度は低く、差分によって得られた \bm v^{t+1} の精度も低くなります。さらに、\bm v^{t+1} は似たような大きさを持つベクトル同士の差分で得られるので、絶対誤差は同程度でも相対誤差は元の位置ベクトルよりも遥かに大きくなります。速度ベクトルは今後の運動を決定する重要なパラメータなので、運動量が全く保存せず謎の外力に支配される、自由落下していたと思ったら突然空間に張り付いたように止まるなど散々な結果となります。

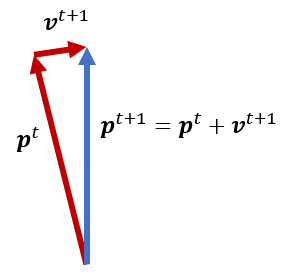
一方、上図のように \bm p^t と \bm v^{t+1} をテクスチャに保存しておき、それらの和によって次の位置ベクトル \bm p^{t+1} を計算するようにするとどうでしょう^[4]。位置ベクトル \bm p^t および \bm p^{t+1} の精度の低さは相変わらずですが、より大きさの小さい速度ベクトル \bm v^{t+1} の精度は（絶対誤差について）高く保たれています。結果として、得られる頂点座標自体の精度は変わらないものの、動きの滑らかさが格段に向上し、ようやくまともなシミュレーションができるようになります。

拘束条件を入れる

一般的な布のシミュレーションと同様に、垂直・水平バネ、斜め方向のバネ、曲げを復元するための一つ飛ばしのバネを導入します。

ただし、これらのバネは通常のバネとしてではなく、頂点間距離に対する拘束条件として計算します。

すなわち、バネの自然長を l、両端の位置ベクトルを \bm p_1,\bm p_2 として、\|\bm p_2-\bm p_1\|=l が常に保たれるように努力するのがこのバネの務めです。安定性を高めるために陰解法を採用すると、時刻 t+1 においてこの式が成り立つ、すなわち \|\bm p_2^{t+1}-\bm p_1^{t+1}\|=l が満たされることが目標となります。前述の理由より \bm p^{t+1}=\bm p^t+\bm v^{t+1} と定められていましたから、これを代入すると

\|(\bm p_2^t+\bm v_2^{t+1})-(\bm p_1^t+\bm v_1^{t+1})\|=l

が得られます。

拘束力を求める

このバネが現在のフレームにおいて加える力積の係数を \lambda とします（ベクトルではなくスカラーです）。通常のバネにかかる力はフックの法則により求まりますが、このバネは厳密にはバネではなく拘束条件ですので、フックの法則は通用しません。適切な大きさの \lambda を求めるために、バネの力積による次のフレームの速度 \bm v^{t+1} の変化分 \Delta \bm v^{t+1}、およびバネの長さ \|\bm p_2^{t+1}-\bm p_1^{t+1}\| の変化分 \Delta\|\bm p_2^{t+1}-\bm p_1^{t+1}\| を求めてみましょう。

バネの伸びている方向を表す単位ベクトルを

\bm n=\frac{\bm p_2^{t+1}-\bm p_1^{t+1}}{\|\bm p_2^{t+1}-\bm p_1^{t+1}\|}

とし（時刻 t+1 における位置ベクトルを用いていることに注意してください）、頂点1にかかる力積を \lambda \bm n、頂点2にかかる力積を -\lambda \bm n とします（作用・反作用の法則）。すると、それぞれの頂点における速度変化は、各頂点の質量 m_1,m_2 を用いて

\Delta \bm v_1^{t+1}&=\frac1{m_1}\lambda \bm n\\
\Delta \bm v_2^{t+1}&=-\frac1{m_2}\lambda \bm n

と表せます。したがって、時刻 t+1 における位置ベクトルの差 \bm p_2^{t+1}-\bm p_1^{t+1} の変化分は

\Delta(\bm p_2^{t+1}-\bm p_1^{t+1})=\Delta\bm v_2^{t+1}-\Delta\bm v_1^{t+1}=-\left(\frac1{m_1}+\frac1{m_2}\right)\lambda\bm n

となります。

ここで、\bm n の定義より、\bm n が \bm p_2^{t+1}-\bm p_1^{t+1} と同じ向きの単位ベクトルであったことを思い出すと、この変化分はそのまま長さの変化分に適用でき、

\Delta\|\bm p_2^{t+1}-\bm p_1^{t+1}\|=-\left(\frac1{m_1}+\frac1{m_2}\right)\lambda

が成り立ちます。ただし、\lambda が2頂点の位置関係をひっくり返すほど大きくなるとこの式は成り立たなくなるため、\lambda が大きすぎないことを仮定します。

結局のところ、バネが加える力積の係数 \lambda を 1 だけ大きくすると、次の時刻におけるバネの長さは 1/m_1+1/m_2 だけ短くなる、という対応関係があることが分かりました。実は、この逆数 (1/m_1+1/m_2)^{-1} には（2頂点間の）換算質量という名前が付いており、この質量は「バネが感じる質量」に相当します。この値が大きいほど、バネが2頂点間の距離を変化させることが難しくなる（＝より大きな \lambda を必要とする）ことが数式から見て取れます。

注意：一般に力積は速度を変化させるもので、位置を直接変化させるものではありません。力積によって各頂点の速度が変化し、その結果として次の時刻におけるバネの長さが変化した、という関係を理解してください。また、本来は加えて時間刻み幅 \Delta t が数式中に出現することに注意してください（今回は \Delta t=1 としたため式が簡単になっています）。

以上より、拘束を満たすために必要な \lambda の値が計算できます。いま、\|\bm p_2^{t+1}-\bm p_1^{t+1}\|=l が成り立っていない（拘束違反）と仮定し、拘束力による補正の結果、拘束違反が解消されるとします。すると、次の式が成り立ちます。

\|\bm p_2^{t+1}-\bm p_1^{t+1}\|+\Delta \|\bm p_2^{t+1}-\bm p_1^{t+1}\|=l

後はそのまま先程の式を代入し、

\|\bm p_2^{t+1}-\bm p_1^{t+1}\|-\left(\frac1{m_1}+\frac1{m_2}\right)\lambda=l\\

より

\lambda=\left(\frac1{m_1}+\frac1{m_2}\right)^{-1}\left(\|\bm p_2^{t+1}-\bm p_1^{t+1}\|-l\right)

を得ます。そして、この値を用いて、次の時刻の速度を正しい値に補正（更新）します。

\bm v_1^{t+1}&\gets\bm v_1^{t+1}+\frac1{m_1}\lambda \bm n\\
\bm v_2^{t+1}&\gets\bm v_2^{t+1}-\frac1{m_2}\lambda \bm n

バネが複数存在する場合に拡張する

以上の計算では、頂点1と頂点2、そしてそれらを繋ぐバネのみが世界に存在すると仮定して計算を行いました。しかし実際には、多数の頂点が多数のバネで繋がるネットワークを形成しています。すなわち、実際のところバネは合計 M 個あり、i 番目のバネが頂点 i_1 と頂点 i_2 を自然長 l_i で結んでいるとして、M 個の拘束条件

\|\bm p_{i_2}^{t+1}-\bm p_{i_1}^{t+1}\|=l_i

を要求しています。このとき、我々が解くべき方程式は未知数 \lambda_1,\dots,\lambda_M に対する非線形な連立方程式となります。

これは非常に大変そうに見えますが、多くの場合は反復法によって解くことができます。連立一次方程式に対する反復解法である Jacobi 法や Gauss-Seidel 法を知っている方は、それらの非線形版を想像してもらえればOKです。

次のような問題を想像してみてください：

一列に並んだ M 本の杭が地面に中途半端に刺さっています。あなたの仕事は、これらの杭を全て地面に埋めることです。あなたはハンマーを持っており、ハンマーで i 番目の杭を叩くと、i 番目の杭は完全に地面に埋まります。しかし、その反動で周辺の杭が地面から少し飛び出ます。全ての杭を完全に地面に埋められますか？

しばらく考えてみると、とにかく全部の杭を叩いて回れば最終的には全部の杭が（ほとんど完全に）地面に埋まった状態になるのが想像できるかと思います。非常に雑ではありますが、これが線形・非線形を問わず多くの反復解法における本質的な原理^[5]です。

現在の状況と照らし合わせてみましょう。

• M 本の杭 \leftrightarrow M 本のバネ
• 杭 i が地面に完全に埋まる \leftrightarrow バネ i の拘束が完全に満たされる
• 杭 i を叩く \leftrightarrow バネ i だけを考えて 拘束力 \lambda_i を求め、速度 \bm v_{i_1}^{t+1},\bm v_{i_2}^{t+1} を更新する
• 杭 i は完全に地面に埋まる \leftrightarrow バネ i だけを考えて拘束を解いた結果、バネ i の拘束は完全に満たされる
• 周辺の杭が地面から少し飛び出る \leftrightarrow 頂点 i_1,i_2 に繋がっているその他のバネの拘束が満たされなくなる
• 全ての杭を完全に地面に埋められますか？ \leftrightarrow 全てのバネの拘束を完全に満たせますか？

というわけで、我々がやるべきは

「バネ i について、他のバネを無視して拘束を解き、頂点 i_1,i_2 の速度を更新する」という手順を、全てのバネ i についてひたすら繰り返す

ということになります。拘束を解くばねの順番を 1,2,\dots,M,1,2,\dots,M,1,2,\dots とループさせれば、反復法は Gauss-Seidel 法に対応します。一般にはループは誤差が十分小さくなったところで打ち切りますが、今回は誤差に関係なく固定回数のループで打ち切っています。

Jacobi 的な反復を行う

しかし、上記の方法には問題点があります。それは、GPU による並列化に対応できないという点です。並列計算においては、全ての拘束を（物理的に）同時刻に解く必要があります。したがって、「まずバネ1について解いて、その結果を見つつバネ2について解いて、…」といった計算が不可能になります。この問題に対するアプローチは

1. 拘束を互いに干渉しないグループに分け、グループ単位で並列に解く
2. もう結果を気にせずに全部並列に解いてしまう

の2種類があります。1番目のアプローチは、例えば Stable Fluids のような格子法における流体計算において、格子を互い違いに2色に塗り分けてグループ化する checkerboard SOR 法（あるいは red-black SOR 法）などの例が知られています。

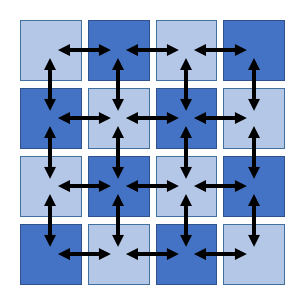
一つの四角が一つの拘束に対応しており、矢印が拘束間の依存関係を表します。図のように2色で塗り分けることにより、互いに干渉しない2つのグループに拘束を分けることができます^[6]。

しかし、今回のような場合は、頂点間を斜めに繋ぐバネや一つ飛ばしで繋ぐバネなどの存在により、少ないグループ数で拘束を綺麗にグループ化することができません。あまりグループ数が増えると同期のオーバーヘッドなどにより並列化のありがたみが減ってしまうため、今回は2番目のアプローチを採用することにしました。

この場合、各バネ i の拘束を解いて \lambda_i を計算するところまでは一緒ですが、その場ですぐに速度を更新せずに、全ての i について \lambda_i が計算し終わるまで更新を先延ばしにします。すべての \lambda_i が求まったら、実際に力積を各頂点に適用し、速度を一斉に更新します。この方法は Jacobi 法に対応します。

並列化への対応が簡単にできる Jacobi 的な手法ですが、収束性能は Gauss-Seidel 的な手法に比べかなり悪化します。すなわち、同じ問題でも Jacobi 的に解く場合は Gauss-Seidel 的に解く場合よりも多くの反復回数を必要とします。また、問題によっては Gauss-Seidel 的に解けば収束するのに、Jacobi 的に解いた場合は発散してしまうこともあります。実は今回の設定でも Jacobi 的に解いた場合は発散してしまいました。

そこで、SOR 法のように緩和係数 \alpha\ (\lt1) を導入し、求めた力積を \alpha 倍したものを実際に各頂点に適用することにします。これにより、解の更新が緩やかになり、Jacobi 的な更新手法でも発散せずに解を求めることができるようになります。最適な緩和係数 \alpha を理論的に求めるのは難しいため、いろいろ試して挙動が不安定にならない範囲でできるだけ大きいものを使っています。

以上の処理を fragment shader で書き、速度テクスチャに複数回の書き込みを行うことで、紙切れを構成する拘束の計算が GPU でできるようになります。

空気抵抗を入れる

ここではあまり真面目な空気力学は考えず、単純化したモデルを使用します。空気抵抗は大まかに次のような特性があります。

• 空気抵抗は風との相対速度が0になるよう加わる
• 相対速度が表面に対して垂直に近いほど大きな抵抗を受ける

これらを満たすように頂点の速度に抵抗を加えます。頂点の法線ベクトルを \bm n、風速ベクトルを \bm v_w、頂点の速度ベクトルを \bm v とします。風との相対速度ベクトルは \bm v_r = \bm v_w-\bm v になります。\bm v_r は次のように分解できます。

• \bm v_r の垂直成分は (\bm n\cdot\bm v_r)\bm n
• \bm v_r の水平成分は \bm v_r - (\bm n\cdot\bm v_r)\bm n

垂直方向の減衰係数 \beta_v、水平方向の減衰係数 \beta_h を適当に決めて、異なる割合で風速に近付けます。

\bm v\gets\bm v+\beta_v (\bm n\cdot\bm v_r)\bm n + \beta_h(\bm v_r - (\bm n\cdot\bm v_r)\bm n)

\beta=0 で抵抗ゼロ、\beta=1 で速度が風速と完全に一致します。今回は \beta_v = 0.1, \beta_h = 0.01 を用いました。

例によって時間刻み幅を考えていないので、フレームレートを変更すると抵抗の大きさも変化します。時間刻み幅に対して指数関数を用いて係数を決定するとフレームレート可変にできそうな気がします。たぶん。

これで空中をヒラヒラ舞ってくれるようになります。

今回は空中（水中？）を漂っているだけなので無重力でしたが、服や旗などのシミュレーションで重力がある場合は、人工的な力として全体に上向きの力を加えるとそれらしく見えるようです^[7]。

とりあえず描画する

各頂点の座標はテクスチャに書き込んであるので、座標の代わりにテクスチャの UV 座標を設定したデータを vertex shader に送り、vertex shader 内でテクスチャを読み込んで出力する座標に設定します (Vertex Texture Fetch, VTF) 。同時に隣接する頂点の座標も読み込んで法線ベクトルを設定しておきます。

後はいつも通り fragment shader で色付けができます。

金色にして適当な外力を作用させてみました。紙吹雪っぽい。まだ外力が適当なので、あまり綺麗には流れてくれません。

流速ベクトル場を用意する

綺麗に対流させたいので、いい感じの流速ベクトル場を用意して風速として扱います。計算負荷を考えると、事前計算しておいて実行時に読み込んで参照する方式がよさそうということで、3次元の Stable Fluids を走らせて解像度 64\times64\times64=512^2 の流速ベクトル場を用意しました。

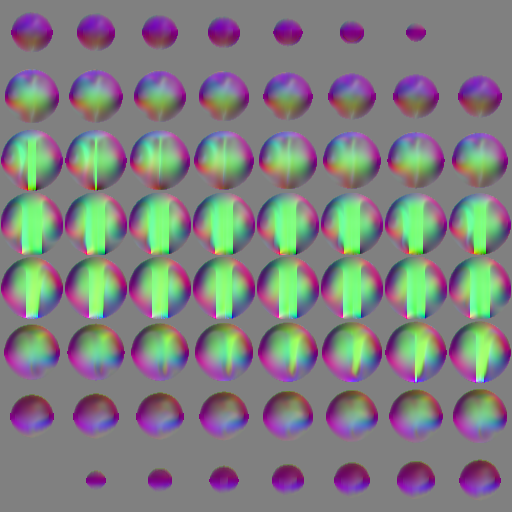
計算された流速場をz軸方向にスライスして並べた画像がこちら。法線マップと同じように \bm v\times0.5+0.5 して0から255に収めてあります。球状のドーム内部を真ん中から吹き上げるようなベクトル場にしてあります。微妙なゆらぎが発生しているのがいいですね。

この画像を読み込んで、fragment shader で参照して流速場として抵抗力を計算します。WebGL の UV 座標系とアップロード時のバイト列の並べ方で混乱してベクトル場が上下左右前後に反転しまくって大変でした。最終的に符号が合ったのでヨシ！

いい感じに見せる

物理演算部分が完成したので、いい感じに見せるための描画処理を作っていきます。背景のグラデーションは fragment shader でカメラからの視線ベクトルの向きを使って色を計算するだけです。

上を向いたときに見える volumetric lighting っぽい効果でやや複雑な処理をしています（といってもぼかしをかけて加算合成するだけですが）。

放射状に差し込む光

光源をマスクする

まず、光らせたい部分だけを切り抜いたテクスチャを作ります。具体的には、光源の周囲のみを明るくしたテクスチャを作り、紙を真っ黒にして上書きします。光源の方を向いていないときは全体が真っ黒になります。テクスチャのサイズは 512×512 固定にしました。

かなり暗く見えますが、後に加算合成されるのでこの程度で十分です。

放射状にぼかす

専用の fragment shader を書いて光源を中心にして放射状にぼかします。

等方的なぼかしと違い、サンプリングを行う方向が1次元なので 1pass でも十分高速に処理できます。UV 座標を指数的に中心に近付けながら40回のサンプリングを行い、重み付き平均を取った値をテクスチャに書き込んでいます。光源の中心座標は CPU 側で計算を行い、uniform 変数として fragment shader に送ります。

加算合成で元のシーンと重ねる

合成前はこんな感じに見えています。これに先程のテクスチャを（適当に引き伸ばしつつ）加算合成で重ねると……

こうなります。光が立体的に見えて綺麗です。合成するシーンと同じ設定で紙による光源の遮蔽をしているので、隙間から光が漏れてくる様子が表現できています。

アスペクト比の変化に対する対応

実はしていません。UV 座標はアスペクト比に関わらず 0～1 に固定されてしまうので、放射状にぼかしをかける時点でぼかしの方向が異方的になってしまうのですが、書き込まれる光源自体もアスペクト比に依存して歪むためか、思ったより見た目に影響がなかったので放置してあります。

完成

というわけで完成です。ふと思い立って作り始めた作品ですが、いい感じに仕上がったため満足しています。集中的に作ったので制作期間は6日ほどでした。