MacCormack 法で Stable Fluids の数値拡散を抑制する

良い方法を知ったので備忘録的なまとめです。
MacCormack 法についてきちんと知りたい方はこちらの論文^[1]等を読んでください。

ここでは Stable Fluids をある程度知っている人向けに概念的な説明と実装方法を書きます。

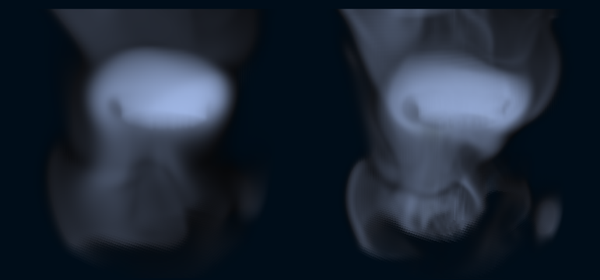
まず冒頭の画像ですが、左側が通常の Semi-Lagrangian 法による計算結果、右側が MacCormack 法を利用した場合の計算結果です。どちらも解像度は同じ 64×64×64 です。細部の表現度合いに圧倒的な差が出ているのが分かるかと思います。

Semi-Lagrangian 法と数値拡散

Stable Fluids の実装では、移流計算に通常は Semi-Lagrangian 法という手法を使います。座標 x における移動量が u のとき、x における物理量を x-u における物理量で更新する、という手法です。「順方向に押し出す」のではなく「逆方向から引っ張ってくる」というイメージですね。通常 x は整数値（セルの真上）になりますが、x-u は半端な値になるため、近接するセルの物理量を引っ張ってきて線形補間します。この方法は GPU における計算と相性が良く、単純に線形補間をかけてテクスチャをサンプリングするだけで実装できます。

しかし、

近接するセルの物理量を引っ張ってきて線形補間します

から予想できる通り、時間経過とともに近接するセル間の物理量が混ざりまくり、あっという間にボケてのっぺりした分布になってしまいます。この現象を数値拡散といいます。物理的には本来発生するはずのない拡散が数値計算によって生じてしまうためです。速度場の数値拡散によって発生する粘性を数値粘性といいます。

Semi-Lagrangian 法による数値拡散はシミュレーションの解像度を上げることで抑制できるのですが、特に3次元の場合は高い解像度で計算することが難しくなります。例えば 256×256×256 の解像度で計算しようとすると、4096×4096 のテクスチャが必要になります。これだけでめちゃ強いデスクトップ環境を除いてまともに動作しなくなります。

そこで役立つのが MacCormack 法です。MacCormack 法を使うと、冒頭の画像のように、解像度はそのままに数値拡散を抑制して細部の表現度を上げることができます。

MacCormack 法

MacCormack 法は一言でいうと「シャープネスフィルタをかけながらの移流計算」です。シャープネスフィルタといっても普通のシャープネスフィルタではなく、ボケた分だけ元に戻そうとする適応的なシャープネスフィルタです。この辺りが非常にうまくできています。

原理としては非常に簡単で、

1. 移流によってボケる量（＝誤差）を予測する (prediction)
2. 実際に移流させ、予測した誤差を引いて打ち消す (correction)

という2ステップからなります。ステップ 1. でいかにうまく予測をするかがカギとなります。

予測は次のように行います。

1. 普通に移流させる
2. その後逆向きに移流させる
3. 元の分布との差を取ると、2回の移流によってボケた量が分かる
4. その半分を1回の移流で生じる誤差とする

単純かつ明快で、最初見たときは天才かと思いました。実装もこの通りに行えばよいです。

計算量も通常の Semi-Lagrangian 法の2～3倍程度です。流体計算のボトルネックは圧力計算部分に集中するため、移流計算が少々重くなったところで大きな影響はありません。

弱点

細部の表現力に絶大な効果を発揮する MacCormack 法ですが、弱点としてアーティファクトが発生します。途中でシャープネスフィルタと書きましたが、誤差の予測が完璧ではないためにちょうどシャープネスフィルタを過剰に掛けたようなアーティファクトが発生します。特に1タイムステップにおける移動量が大きいほどアーティファクトが強く出ます。恐らく誤差の予測が現在の分布に基づいて行われるためでしょう。

それに伴い、物理量の値が上限・下限を突破します。Semi-Lagrangian 法では線形補間により移流を行うため、今ある物理量の最大・最小値を超える値は出現しようがありませんが、MacCormack 法ではそのような制約はありません。そのため、移流後に必要に応じて物理量のクランプを行うことがあるようです。幸い、値のクランプによって著しく性能が悪化することはありません。

また、予測が大きく外れがちな境界付近ではうまく動作しないようで、境界付近では Semi-Lagrangian 法に切り替えないとシミュレーションが爆発することがあるようです。境界付近での切り替えはごく簡単に行えるので、MacCormack 法を導入する場合は忘れずに切り替えるコードも書いておきましょう。

それから、試してみたところ速度場の移流に関しては MacCormack 法を適用しない方が良いことが分かりました。アーティファクトの影響が強く出てシミュレーションが下の画像のように不安定化します。速度場の表現力を上げたい場合は Vorticity Confinement など他の手法を組み合わせて使う方がよさそうです。

追記：Vorticity Confinement の解説記事を書きました

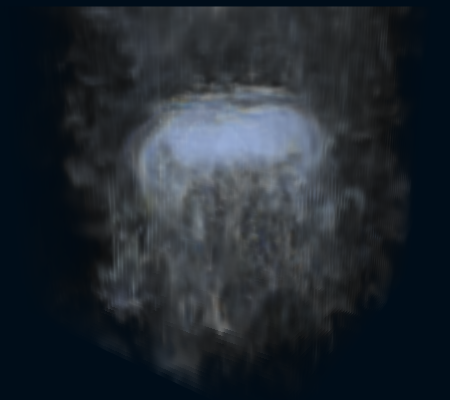
もじゃもじゃしてしまった図

おわり

いくつか難点はありますが、うまく使えば MacCormack 法は多大な威力を発揮します！
これから移流計算を行う予定のある方は導入してみてはいかがでしょうか。